Page 130 - C112214

122

تیلاعف

و هتسویپ (a , b) رب f و دشاب f عبات ینارحب هطقن کی c ∈ (a , b) ⊆ D f مینک ضرف
ٔ
.دشاب ریذپ قتشم c رد لاامتحا زج هب
ً
y

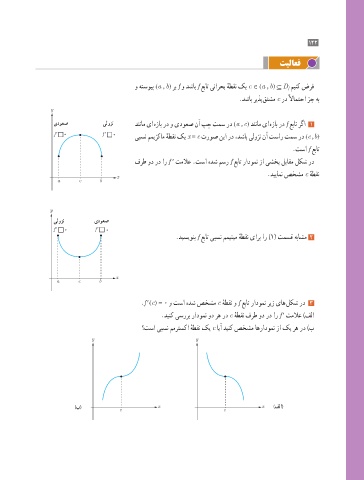
یدوعص یلوزن دننام یا هزاب رد و یدوعص نآ پچ تمس رد (a , c) دننام یا هزاب رد f عبات رگا 1
f ′ 0 f ′ 0 یبسن ممیزکام هطقن کی x = c تروص نیا رد ،دشاب یلوزن نآ تسار تمس رد (c , b)
ٔ
.تسا f عبات

فرط ود رد ار f ′ تملاع .تسا هدش مسر f عبات رادومن زا یشخب لباقم لکش رد
.دییامن صخشم c هطقن
x ٔ
a c b

y

یلوزن یدوعص
f ′ 0 f ′ 0
.دیسیونب f عبات یبسن ممینیم هطقن یارب ار )1( تمسق هباشم 2
ٔ

x
a c b

.f ′ (c) = 0 و تسا هدش صخشم c هطقن و f عبات رادومن ریز یاه لکش رد 3
ٔ
.دینک یسررب رادومن ود ره رد c هطقن فرط ود رد ار f ′ تملاع )فلا
ٔ
؟تسا یبسن ممرتسکا هطقن کی c ایآ دینک صخشم اهرادومن زا کی ره رد )ب
ٔ
y y

)ب( x x )فلا(
c c