Page 136 - C112214

128

تیلاعف

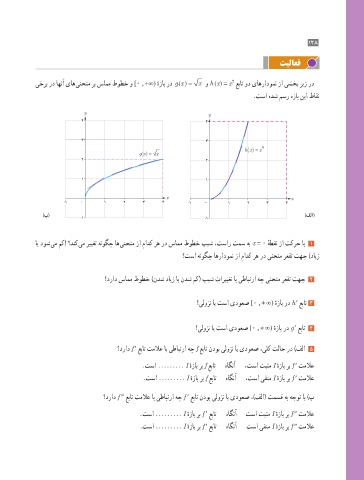
2
gx
یخرب رد اهنآ یاه ینحنم رب سامم طوطخ و ]0 , +∞( هزاب رد () = x و h (x) = x عبات ود یاهرادومن زا یشخب ریز رد
ٔ
.تسا هدش مسر هزاب نیا طاقن
y y
4 4

3 3
=
h(x) x 2
g x x
( ) =
2 2
1 1

x x
-1 0 1 2 3 4 -1 0 1 2 3 4
)ب( )فلا(
-1 -1

ای دوش یم مک( ؟دنک یم رییغت هنوگچ اه ینحنم زا مادک ره رد سامم طوطخ بیش ،تسار تمس هب x = 0 هطقن زا تکرح اب 1
ٔ
؟تسا هنوگچ اهرادومن زا مادک ره رد ینحنم رعقت تهج )دایز

؟دراد سامم طوطخ )ندش دایز ای ندش مک( بیش تارییغت اب یطابترا هچ ینحنم رعقت تهج 2

؟یلوزن ای تسا یدوعص [0 , + ∞( هزاب رد h ′ عبات 3
ٔ

؟یلوزن ای تسا یدوعص [0 , + ∞( هزاب رد g ′ عبات 4
ٔ

؟دراد f ′ عبات تملاع اب یطابترا هچ f عبات ندوب یلوزن ای یدوعص ،یلک تلاح رد )فلا 5
.تسا ......... I هزاب رب f عبات هاگنآ ،تسا تبثم I هزاب رب f ′ تملاع

ٔ ٔ
.تسا ......... I هزاب رب f عبات هاگنآ ،تسا یفنم I هزاب رب f ′ تملاع
ٔ ٔ
؟دراد f ″ عبات تملاع اب یطابترا هچ f ′ عبات ندوب یلوزن ای یدوعص ،)فلا( تمسق هب هجوت اب )ب

.تسا ......... I هزاب رب f ′ عبات هاگنآ تسا تبثم I هزاب رب f ″ تملاع
ٔ ٔ
.تسا ......... I هزاب رب f ′ عبات هاگنآ تسا یفنم I هزاب رب f ″ تملاع
ٔ ٔ