Page 138 - C112214

130

D =  میراد )ب
g
′
2
3
2
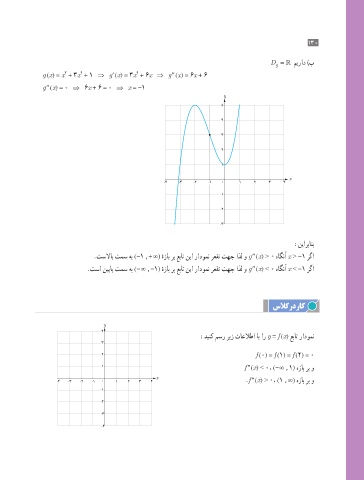
g (x) = x + 3x + 1 ⇒ g (x) = 3x + 6x ⇒ g ″ (x) = 6x + 6
g ″ (x) = 0 ⇒ 6x + 6 = 0 ⇒ x = -1
y
5
4

3

2

1

x
-4 -3 -2 -1 0 1 2 3 4
-1

-2

-3

:نیاربانب
.تسلااب تمس هب (-1 , + ∞( هزاب رب عبات نیا رادومن رعقت تهج اذل و g ″ (x) > 0 هاگنآ x > -1 رگا
ٔ
.تسا نییاپ تمس هب (- ∞ , -1) هزاب رب عبات نیا رادومن رعقت تهج اذل و g ″ (x) < 0 هاگنآ x < -1 رگا
ٔ

سلاکردراک

y
4
:دینک مسر ریز تاعلاطا اب ار y = f (x) عبات رادومن
3
2 f (0) = f (1) = f (2) = 0
1 f ″ (x) < 0، (- ∞ , 1) هزاب رب و

x
-4 -3 -2 -1 0 1 2 3 4 .f ″ (x) > 0، (1 , ∞( هزاب رب و
-1

-2
-3
-4