Page 14 - C112214

6

یدومع ضابقنا و طاسبنا

تیلاعف

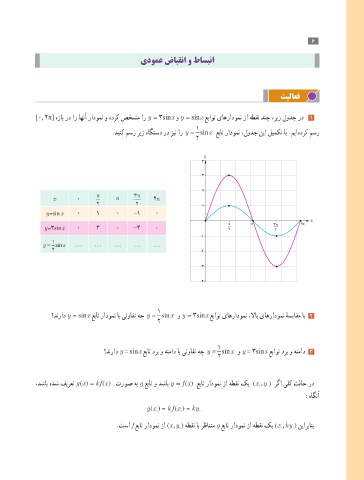
[0, 2π] هزاب رد ار اهنآ رادومن و هدرک صخشم ار y = 3sin x و y = sin x عباوت یاهرادومن زا هطقن دنچ ،ریز لودج رد 1
1
.دینک مسر ریز هاگتسد رد زین ار = sinx عبات رادومن ،لودج نیا لیمکت اب .میا هدرک مسر
y
2
y
4
3

2
π 3 π
x 0 π 2π
2 2 1
y =sin x 0 1 0 -1 0
x
0 π π 3 π 2π
y =3sin x 0 3 0 -3 0 2 2
-1
1
y = sinx ... ... ... ... ...
2 -2

-3

-4

1
؟دنراد y = sin x عبات رادومن اب یتوافت هچ = sinx و y = 3sin x عباوت یاهرادومن ،لااب یاهرادومن هسیاقم اب 2
y
ٔ
2

1
؟دنراد y = sin x عبات درب و هنماد اب یتوافت هچ y = sinx و y = 3sin x عباوت درب و هنماد 3
2

،دشاب هدش فیرعت g (x) = k f (x) تروص هب g عبات و دشاب y = f (x) عبات رادومن زا هطقن کی (x , y ) رگا یلک تلاح رد
0 0
:هاگنآ
g (x ) = k f (x ) = k y
0 0 0
.تسا f عبات رادومن زا (x, y ) هطقن اب رظانتم g عبات رادومن زا هطقن کی (x , k y ) نیاربانب
0 0 0