Page 140 - C112214

132

4
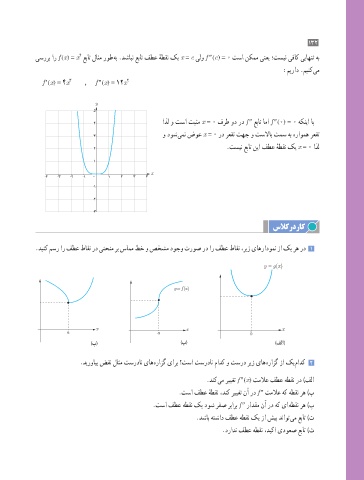
یسررب ار f (x) = x عبات لاثم روط هب .دشابن عبات فطع هطقن کی x = c یلو f ″ (c) = 0 تسا نکمم ینعی ؛تسین یفاک ییاهنت هب
ٔ
:میراد .مینک یم
f ′ (x) = 4x 3 , f ″ (x) = 12x 2

y
5
اذل و تسا تبثم x = 0 فرط ود رد f ″ عبات اما f ″ (0) = 0 هکنیا اب
4
و دوش یمن ضوع x = 0 رد رعقت تهج و تسلااب تمس هب هراومه رعقت
3
.تسین عبات نیا فطع هطقن کی x = 0 اذل
2 ٔ

1
x
-4 -3 -2 -1 0 1 2 3 4
-1
-2

-3
سلاکردراک

.دینک مسر ار فطع طاقن رد ینحنم رب سامم طخ و صخشم دوجو تروص رد ار فطع طاقن ،ریز یاهرادومن زا کی ره رد 1

y = gx
()

()
y= fx

x x x
a a b
)پ( )ب( )فلا(

.دیروایب ضقن لاثم تسردان یاه هرازگ یارب ؟تسا تسردان مادک و تسرد ریز یاه هرازگ زا کی مادک 2

.دنک یم رییغت f ″ (x) تملاع فطع هطقن رد )فلا

.تسا فطع هطقن ،دنک رییغت نآ رد f ″ تملاع هک هطقن ره )ب
ٔ
.تسا فطع هطقن کی دوش رفص ربارب f ″ رادقم نآ رد هک یا هطقن ره )پ
.دشاب هتشاد فطع هطقن کی زا شیب دناوت یم عبات )ت

.درادن فطع هطقن ،دیکا یدوعص عبات )ث