Page 141 - C112214

133 قتشم یاهدربراک : مجنپ لصف

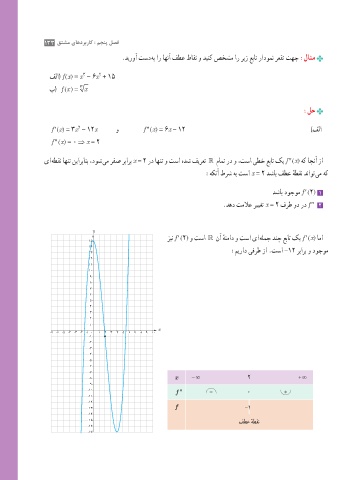
.دیروآ تسد هب ار اهنآ فطع طاقن و دینک صخشم ار ریز عبات رادومن رعقت تهج :لاثم

3
2
فلا( f (x) = x - 6x + 15
ب( ()f x = 3 x

:لح

2
f ′ (x) = 3x - 12x و f ″ (x) = 6x - 12 )فلا
f ″ (x) = 0 ⇒ x = 2

یا هطقن اهنت نیاربانب ،دوش یم رفص ربارب x = 2 رد اهنت و تسا هدش فیرعت  مامت رد و ،تسا یطخ عبات کی f ″ (x) هک اجنآ زا

:هکنآ طرش هب تسا x = 2 دشاب فطع هطقن دناوت یم هک
ٔ

دشاب دوجوم f ′ (2) 1
.دهد تملاع رییغت x = 2 فرط ود رد f ″ 2

y
زین f ′ (2) و تسا  نآ هنماد و تسا یا هلمج دنچ عبات کی f ′ (x) اما
15 ٔ
14
13 :میراد یفرط زا .تسا -12 ربارب و دوجوم
12
11
10
9
8
7
6
5
4
3
2
1
x
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
-1
-2
-3
-4
-5
-6
-7
x - ∞ 2 + ∞
-8
-9
f ″ - 0 +
-10
-11
-12
-13 f -1
-14
-15 فطع هطقن
-16 ٔ
-17