Page 15 - C112214

7 عبات : لوا لصف

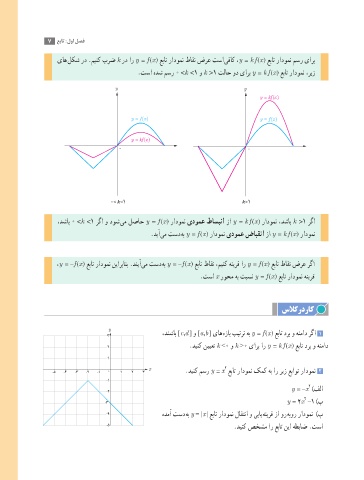
یاه لکش رد .مینک برض k رد ار y = f (x) عبات رادومن طاقن ضرع تسا یفاک ،y = k f (x) عبات رادومن مسر یارب

.تسا هدش مسر 0 <k <1 و k >1 تلاح ود یارب y = k f (x) عبات رادومن ،ریز

y y
x
y = kf ()

y = fx y = fx
()
()
y = kf ()
x
0 0

0< k <1 k >1

،دشاب 0 <k <1 رگا و دوش یم لصاح y = f (x) رادومن یدومع طاسبنا زا y = k f (x) رادومن ،دشاب k >1 رگا

.دیآ یم تسد هب y = f (x) رادومن یدومع ضابقنا زا y = k f (x) رادومن

،y = -f (x) عبات رادومن نیاربانب .دنیآ یم تسد هب y = -f (x) عبات طاقن ،مینک هنیرق ار y = f (x) عبات طاقن ضرع رگا

.تسا x روحم هب تبسن y = f (x) عبات رادومن هنیرق

سلاکردراک

y

3 ،دنشاب [c,d ] و [a,b ] یاه هزاب بیترت هب y = f (x) عبات درب و هنماد رگا 1
2 .دینک نییعت k >0 و k <0 یارب ار y = k f (x) عبات درب و هنماد

1
x 2
-5 -4 -3 -2 -1 0 1 2 3 .دینک مسر y = x عبات رادومن کمک هب ار ریز عباوت رادومن 2
-1
2
y = -x )فلا
-2
2
-3 y = 2x -1 )ب
-4 هدمآ تسد هب y = | x | عبات رادومن لاقتنا و یبای هنیرق زا ور هبور رادومن )پ
-5 .دینک صخشم ار عبات نیا هطباض .تسا