Page 150 - C112214

142

میراد (1 , +∞) هزاب رد x ره یارب و نییاپ تمس هب ینحنم رعقت اذل ،f ″ (x) < 0 میراد (- ∞ , 1) هزاب رد x ره یارب نیاربانب
ٔ ٔ
:تسا ریز تروص هب عبات راتفر لودج .تسلااب تمس هب ینحنم رعقت اذل و f ″ (x) > 0

x - ∞ -2 0 1 + ∞
y ′ - - - -

y ″ - - - +

y 0 -2 - ∞ + ∞

y
7
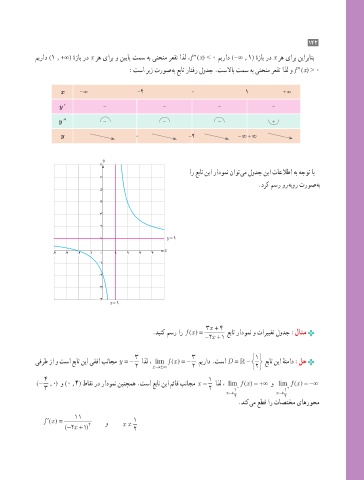
ار عبات نیا رادومن ناوت یم لودج نیا تاعلاطا هب هجوت اب
6
.درک مسر ور هبور تروص هب
5

4
3

2
1 y =1
x
-4 -3 -2 -1 0 1 2 3 4
-1
-2

-3
-4
x =1

3 x + 4
.دینک مسر ار ()f x = عبات رادومن و تارییغت لودج :لاثم
− x +2 1

3 3 
1
یفرط زا و تسا عبات نیا یقفا بناجم y = − اذل ، lim f ( ) = − میراد .تسا = D −  عبات نیا هنماد :لح
x
2 x→±∞ 2  ٔ
2
4 1
(− ,) و (0 , 4) طاقن رد رادومن نینچمه .تسا عبات نیا مئاق بناجم = اذل ، lim ( ) = +∞ و lim ( ) = −∞
f
x
x
0
x
f
3 2 1 − 1 +
x→ x→
2 2
.دنک یم عطق ار تاصتخم یاهروحم
11
() =
′ fx و x ≠ 1
(− + x 2 ) 1 2
2