Page 18 - C112214

10

سلاکردراک

k > 0 و k < 0 یارب ار y = f (k x) عبات درب و هنماد ،دنشاب [c,d ] و [a,b ] یاه هزاب بیترت هب y = f (x) عبات درب و هنماد رگا 1

.دینک نییعت
y
4
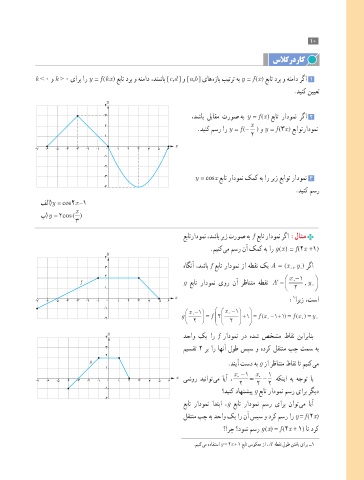
3 ،دشاب لباقم تروص هب y = f (x) عبات رادومن رگا 2

2 x
.دینک مسر ار y = f (- ) و y = f (3x) عباوترادومن

1 2
x
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
-1
-2
-3
y = cos x عبات رادومن کمک هب ار ریز عباوت رادومن 3
-4
.دینک مسر

فلا(y = cos 2 x-1
x
ب( = 2 cos( )
y
3
عباترادومن ،دشاب ریز تروص هب f عبات رادومن رگا :لاثم

.مینک یم مسر نآ کمک هب ار g (x) = f (2x +1)
y
4
هاگنآ ،دشاب f عبات رادومن زا هطقن کی A = (x , y ) رگا
3 0 0
2  x −1 
f g عبات رادومن یور نآ رظانتم هطقن A′ =  0 , y 
1  2 0 
x 1
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 : اریز ،تسا
-1  x −1  x −   1  
() y
11
g 0 = f  0  2 1 = ( f x −+ ) = f x =
-2   +     0 0 0
 2    2  
y
4 دحاو کی ار f رادومن رد هدش صخشم طاقن نیاربانب
3 میسقت 2 رب ار اهنآ لوط سپس و هدرک لقتنم پچ تمس هب
2
g .دنیآ تسد هب g زا رظانتم طاقن ات مینک یم
1
x −1 x 1
x یشور دیناوت یم ایآ ، 0 = 0 − هکنیا هب هجوت اب
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 2 2 2
-1
؟دینک داهنشیپ g عبات رادومن مسر یارب رگید
-2
عبات رادومن ادتبا ،g عبات رادومن مسر یارب ناوت یم ایآ
لقتنم پچ هب دحاو کی ار نآ سپس و درک مسر ار y = f (2x)

؟ارچ ؟دوش مسر g (x) = f (2x + 1) ات درک

.مینک یم هدافتسا y = 2x + 1 عبات سوکعم زا ،A′ هطقن لوط نتفای یارب ــ1