Page 21 - C112214

2 میسقت و یریذپ شخب و اونکی عباوت ،موس هجرد عبات

سرد

،...،a ،a ،a و یفنمان حیحص ددع کی n دینک ضرف
عبات .a n ≠0 هک دنشاب یقیقح دادعا a n و a n -1 0
2 1
1 .دوش یم هدیمان n هجرد زا یا هلمج دنچ عبات ،دوش یم فیرعت ریز تروص هب هک f (x)

2
...
n -1
n x + +a x +a x +a

f (x) = a n x + a n -1 2 1 0
کی ،m ≠0 هک f (x) = m x +b یطخ عبات و رفص هجرد زا یا هلمج دنچ عبات کی ،f (x) = c تباث عبات

2
عبات کی f (x) = a x +bx +c هلداعم هب یمهس کی بیترت نیمه هب .تسا کی هجرد زا یا هلمج دنچ عبات

.تسا ود هجرد زا یا هلمج دنچ
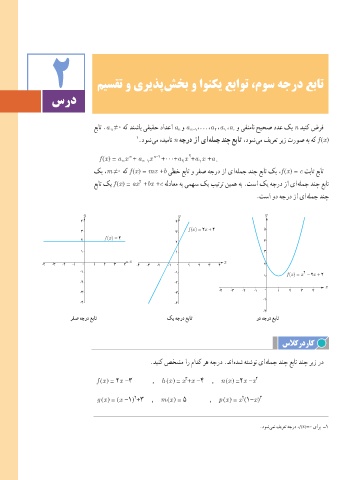
y y y
4 4
fx x + 2 5
() = 2
3 3
fx
() = 2
2 4
2
1 1 3
x x
-4 -3 -2 -1 0 1 2 3 4 -4 -3 -2 -1 0 1 2 3 4 2
-1 -1 2
() =
1 fx x − x + 2 2
-2 -2
x
-3 -3 -4 -3 -2 -1 0 1 2 3 4
-1
-4 -4
-2
رفص هجرد عبات کی هجرد عبات ود هجرد عبات

سلاکردراک

.دینک صخشم ار مادک ره هجرد .دنا هدش هتشون یا هلمج دنچ عبات دنچ ریز رد

3
f (x ) = 2x -3 , h (x ) = x +x -4 , n (x ) =2x -x 4

g (x ) = (x -1) +3 , m (x ) = 5 , p (x ) = x (1-x ) 3
2
2

.دوش یمن فیرعت هجرد ،f (x)=0 یارب ــ1