Page 37 - C112214

29 تاثلثم : مود لصف

دیاب b و a یود ره ،دراد y و x یاهروحم هب تبسن عبات رادومن ندش هنیرق رب b و a زا مادک ره ندوب یفنم هک یریثأت هب هجوت اب
y = 3sin (2 x) +٤ :تسا لباقم تروص هب رظن دروم عبات هطباض اذل دنشاب تبثم
ٔ

و ممینیم و ممیزکام ریداقم هب هجوت اب و دشاب y = a sin bx + c تروص هب دناوت یم رظن دروم عبات هطباض ،رادومن هب هجوت اب )ب
ٔ
1
.تسا )یفنم( تبثم b و )تبثم( یفنم a تملاع نآ رد هک دیآ یم تسد هب |b | = 3 و ||a = و c = 0 ،رادومن یور زا بوانت هرود
ٔ
1 2
y = − sin x :میراد نیاربانب
3
2
5 ربارب نآ ممینیم و ممیزکام ریداقم و دشاب y = a cos bx + c تروص هب دناوت یم رظن دروم عبات هطباض ،رادومن لکش هب هجوت اب )پ
ٔ
x 1 1
. y = 2 cos( ) + 3 :میراد نیاربانب و b = و a = 2 اذل |a | = 2 و ||b = و c = 3 نیاربانب .تسا 4π ربارب بوانت هرود و 1 و
ٔ
2 2 2
.تسا تبثم b و یفنم a و |b | = 1 و |a | = 2 و c = 0 و دشاب y = a cos bx + c تروص هب دناوت یم زین رادومن نیا هطباض )ت
ٔ
y = -2cos x :میراد نیاربانب

تناژنات

تیلاعف

′
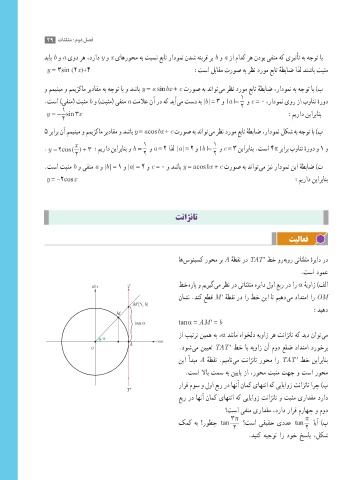
اه سونیسک روحم رب A هطقن رد TAT طخ ور هبور یتاثلثم هریاد رد
ٔ
ٔ
.تسا دومع
ٔ
sin T طخ هراپ و میریگ یم رظن رد یتاثلثم هریاد لوا عبر رد ار α هیواز )فلا
ناشن .دنک عطق M ′ هطقن رد ار طخ نیا ات میهد یم دادتما ار OM
ٔ
1
(, )
M' b
:دیهد
M
tan α tan α = AM ′ = b
زا بیترت نیمه هب ،α دننام هاوخلد هیواز ره تناژنات هک دید ناوت یم
α cos
A
O .دوش یم نییعت TAT ′ طخ اب هیواز نآ مود علض دادتما دروخرب
نیا أدبم A هطقن .میمان یم تناژنات روحم ار TAT ′ طخ نیاربانب
ٔ
.تسا لااب تمس هب نییاپ زا ،روحم تبثم تهج و تسا روحم
رارق موس و لوا عبر رد اهنآ نامک یاهتنا هک ییایاوز تناژنات ارچ )ب
T'
عبر رد اهنآ نامک یاهتنا هک ییایاوز تناژنات و تبثم یرادقم دراد

؟تسا یفنم یرادقم ،دراد رارق مراهچ و مود
3 π π
کمک هب ؟روطچ tan ؟تسا یقیقح یددع tan ایآ )پ
2 2
.دینک هیجوت ار دوخ خساپ ،لکش