Page 41 - C112214

3 y
2
1
x
-4π -3π -2π -π 0 π 2π 3π 4π
-1
33 تاثلثم : مود لصف
-2
-3
y نیرمت
3
2
.دیروآ تسد هب ار ریز عباوت زا کی ره ممینیم و ممیزکام ریداقم و بوانت هرود 1
1
x
فلا( y = 1 + 2 sin 7x -3π -2π -π 0 π 2π 3π 4π
-4π
-1
π -2
ب( y = 3 − cos x -3
2
x
پ( y = −π sin( ) −2
2 y
3 3
ت( y =− cos x 2
3
4
1
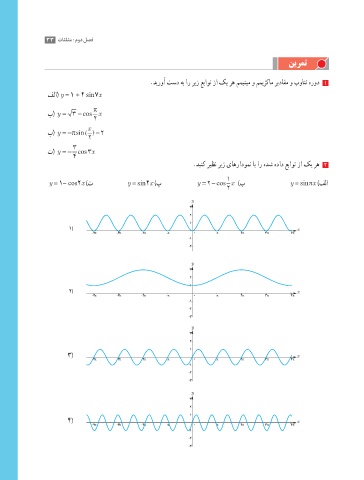
.دینک ریظن ریز یاهرادومن اب ار هدش هداد عباوت زا کی ره 2
x
-4π -3π -2π -π 0 π 2π 3π 4π
-1 1
2
y = 1- cos2x )ت y = sin 2x )پ -2 y =− cos x )ب y = sin πx )فلا
y 2
-3
3
2 y y
3 3
1
2 2 x
-4π -3π -2π -π 1 1 0 π 2π 3π 4π
-1
١( x x
-2π
-3π
2π
3π
4π
-4π -3π -2π -π -π -2 0 0 π π 2π 3π 4π
-4π
-1 -1
-3
-2 -2
y
-3 -3
3
y
2
3
1
2 x
-4π -3π -2π -π 1 0 π 2π 3π 4π
-1
2( x
-4π -3π -2π -π -2 0 π 2π 3π 4π
-1
-3
-2
-3
y
3
y
2
3
1
٣( 2 x
-4π -3π -2π -π 0 π 2π 3π 4π
1
-1
-4π -3π -2π -π -2 0 π 2π 3π 4π x
-1
-3
-2
y
-3 y
3
3
2 y
2 3
1
1 2
٤( -4π -3π -2π -π 0 π 2π 3π 4π x x
-4π -3π -2π -π 1 0 π 2π 3π 4π
-1
-1 x
-4π -3π -2π -π -2 0 π 2π 3π 4π
-2
-1
-3
-3
-2
-3 y
3
2
1
x
-4π -3π -2π -π 0 π 2π 3π 4π
-1
-2
-3
y
3
2
1
x
-4π -3π -2π -π 0 π 2π 3π 4π
-1
-2
-3
y
3
2
1
x
-4π -3π -2π -π 0 π 2π 3π 4π
-1
-2
-3