Page 45 - C112214

37 تاثلثم : مود لصف

sin x = a هلداعم نیاربانب .sin α=a میراد نآ یارب هک دراد دوجو α دننام یا هیواز ،sinx =a هک -1≤ a ≤1 یقیقح ددع یارب
ار α و x یاه نامک نیب هطبار دیاب sin x =sin α هلداعم یاه باوج نتفای یارب نونکا .دوش یم یسیونزاب sin x = sin α تروص هب

.میبایب
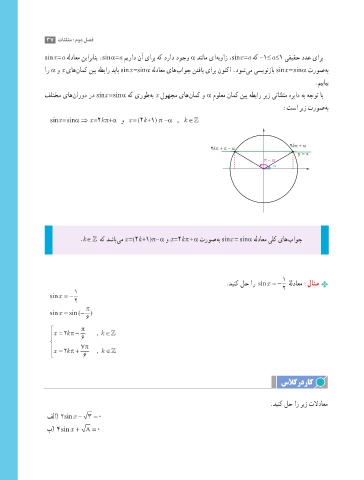
فلتخم یاه نارود رد sinx = sin α هک یروط هب x لوهجم یاه نامک و α مولعم نامک نیب هطبار ریز یتاثلثم هریاد هب هجوت اب

:تسا ریز تروص هب
sinx = sinα ⇒ x =2k π+α و x = (2k +1) π -α , k ∈

2 kπ+ π−α 2 kπ+ α
y = a
π−α
α

.k ∈ هک دشاب یم x =(2k +1)π- α و x =2k π + α تروص هب sinx = sinα هلداعم یلک یاه باوج

1
.دینک لح ار sin = − هلداعم :لاثم
x
ٔ
1 2
sin = −
x
2
π
sin = sin(− )
x
6
 π
 x = 2 kπ − 6 , k ∈

 x = 2 kπ + 7 π , k ∈
 6

سلاکردراک

.دینک لح ار ریز تلاداعم
فلا( sinx −2 = 30
=
ب( sinx4 + 80