Page 56 - C112214

48

.داد هئارا ناوت یم ار ریز فیرعت دش هدهاشم لبق هحفص سلاک رد راک و تیلاعف رد هچنآ هب هجوت اب
ٔ

یهانتمان هفرط کی یاهدح فیرعت

نیدب lim ( ) = +∞f x تروص نیا رد دشاب هدش فیرعت a دننام یا هطقن تسار یگیاسمه کی رد f عبات مینک ضرف
x →a +
تمس زا ار x هک یطرش هب مینک رت گرزب یتبثم ددع ره زا میهاوخب ردق ره هاوخلد هب ار f (x) میناوت یم هک تسا ینعم

.میشاب هدرک کیدزن a هب یفاک هزادنا هب تسار

lim ( ) = +∞f x تروص نیا رد دشاب هدش فیرعت a دننام یا هطقن پچ یگیاسمه کی رد f عبات مینک ضرف نینچمه
x →a −
زا ار x هک یطرش هب مینک رت گرزب یتبثم ددع ره زا میهاوخب ردق ره هاوخلد هب ار f (x) میناوت یم هک تسا ینعم نیدب

.میشاب هدرک کیدزن a هب یفاک هزادنا هب پچ تمس

x
f
فیصوت .تسا قوف فیراعت هباشم زین lim ( ) = −∞f x و lim ( ) = −∞ یهانتمان هفرط کی یاهدح فیرعت :رکذت
x →a − x →a +
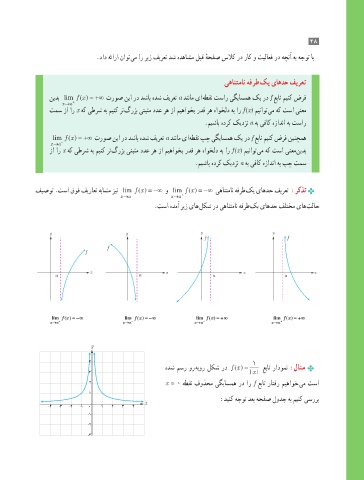
.تسا هدمآ ریز یاه لکش رد یهانتمان هفرط کی یاهدح فلتخم یاه تلاح

y y y y
f f
f
f

x x x x
a a a a

( )
( )
( )
( )
lim fx = −∞ lim fx = −∞ lim fx = +∞ lim fx = +∞
x→ a + x→ a − x→ a − x→ a +
y

4 1
هدش مسر ور هبور لکش رد () = عبات رادومن :لاثم
x
f
3 || x
2 x = 0 هطقن فوذحم یگیاسمه رد ار f عبات راتفر میهاوخ یم تسا
1
:دینک هجوت دعب هحفص لودج هب مینک یسررب
x
-4 -3 -2 -1 0 1 2 3 4
-1
-2
-3