Page 58 - C112214

50

سلاکردراک

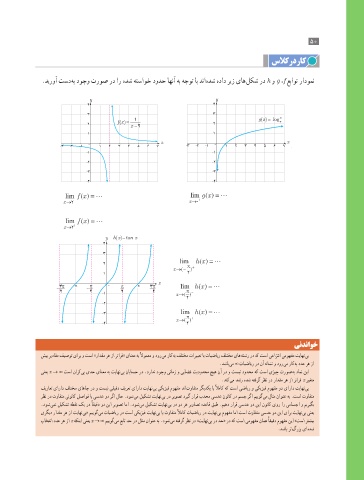
.دیروآ تسد هب دوجو تروص رد ار هدش هتساوخ دودح اهنآ هب هجوت اب دنا هدش هداد ریز یاه لکش رد h و g ،f عباوت رادومن

=
=
y
y y y y y h(x) tan x h(x) tan x
4 4 4 4 4 4
3 3 3 3 x x 3 3
( )=
( )=
()=
()=
fx 1 fx 1 gx log 3 gx log 3
2 2 2 2 2 2
x −2 x −2
1 1 1 1 1 1
x x x x x x
-3 -2 -1 -3 0 -2 1 -1 2 0 3 1 4 2 5 3 6 4 7 5 -3 6 -2 7 -1 -3 0 -2 1 -1 2 0 3 1 4 2 5 3 6 4 7 5 3 6 π 7 -π 3 π π -π 0 π π 0 π π 3 π π 3 π
− − − −
-1 -1 -1 -1 2 2 2 -1 2 2 -1 2 2 2
-2 -2 -2 -2 -2 -2
-3 -3 -3 -3 -3 -3
-4 -4 -4 -4 -4 -4
lim ( ) =  lim ( ) = 
gx
f
x
x →2 − x →0 +
lim ( ) = 
x
f
x →2 +
=
y y y h(x) tan x
4 4 4
3 3 x 3
( )=
( ) =
()=
2 fx 1 2 gx log 3 2 lim hx
x −2 π +
x →− )
(
1 1 1 2
x x x
( ) =
-3 -2 -1 0 1 2 3 4 5 6 7 -3 -2 -1 0 1 2 3 4 5 6 7 3 π -π π 0 π π 3 π lim hx
− −
π
-1 -1 2 2 -1 2 2 x → () −
2
-2 -2 -2
( ) =
-3 -3 -3 lim hx
π
x → () +
-4 -4 -4 2
یندناوخ
شیب ریداقم فیصوت یارب و تسا »رادقم ره زا رتارف« یانعم هب ً لاومعم و دور یم راک هب فلتخم تاریبعت اب تایضایر فلتخم یاه هتشر رد هک تسا یعازتنا یموهفم تیاهن یب
.دشاب یم ∞ تایضایر رد نآ هناشن و دور یم راک هب ددع ره زا
ینعی x → ∞ تسا نارک یب یدح یانعم هب تیاهن یب ناباسح رد .درادن دوجو ینامز و ییاضف تیدودحم چیه نآ رد و تسین دودحم هک تسا یزیچ تروص هب دامن نیا
.دنک یم دشر هدش هتفرگ رظن رد رادقم ره زا رتارف x ریغتم
فیراعت یاراد فلتخم یاهاج رد و تسین یقیقد فیرعت یاراد تیاهن یب یکیزیف موهفم دنا توافتم رگیدکی اب ً لاماک هک تسا یضایر و یکیزیف موهفم ود یاراد تیاهن یب
رظن رد توافتم ینوناک لصاوف اب یسدع ود رگا لاح .دوش یم لیکشت تیاهن یب رد ریوصت دریگ رارق بدحم یسدع نوناک رد مسج رگا مییوگ یم لاثم ناونع هب .تسا توافتم
.دوش یمن لیکشت هطقن کی رد ًاقیقد ود نیا ریوصت اما .دوش یم لیکشت تیاهن یب رد ود ره ریواصت هدعاق قبط .میهد رارق یسدع ود نیا نوناک یور ار یماسجا و میریگب
یرگید رادقم ره زا تیاهن یب« مییوگ یم تایضایر رد تسا یکیزیف تیاهن یب اب توافتم ً لاماک تایضایر رد تیاهن یب موهفم اما تسا توافتم یسدع ود نیا یارب تیاهن یب ینعی
باختنا ددع ره زا x هکنیا ینعی x → ∞ مییوگ یم عبات دح رد لاثم ناونع هب .دوش یم هتفرگ رظن رد »تیاهن یب رد دح« رد هک تسا یموهفم نامه ًاقیقد موهفم نیا »تسا رتشیب
.دشاب رت گرزب یا هدش