Page 59 - C112214

51 تیاهن یب رد دح ـ یهانتمان یاهدح : موس لصف

1 تیاهن یب یاهدح یایاضق زا یخرب

:هاگ نآ ؛دشاب یعیبط ددع کی n رگا :١ هیضق


lim 1 = +∞ و lim 1 =  +∞ ،دشاب جوز یددع n
x→0 + x n x→0 − x n  −∞ ،دشاب درف یددع n

:تشون ناوت یم قوف هیضق هب هجوت اب :لاثم

1 1 1
lim = +∞ و lim = +∞ lim = −∞
−
0
x→0 + x 4 x → x 4 x→0 − x 3
f
f
x
f
x
x
.سکعرب و lim ( ) = +∞ هاگ نآ lim ( ) = +∞ و lim ( ) = +∞ رگا )فلا :2 هیضق
x→ a x→ a − x→ a +
.سکعرب و lim ( )f x = −∞ هاگ نآ lim ( )f x = −∞ و lim ( )f x = −∞ رگا )ب
x→ a x→ a − x→ a +
2 2 2
lim = +∞ هجیتن رد و lim = +∞ و lim = +∞ :لاثم
| −1
| −1
| −1
1
x → x | x →1 − x | x →1 + x |
سلاکردراک

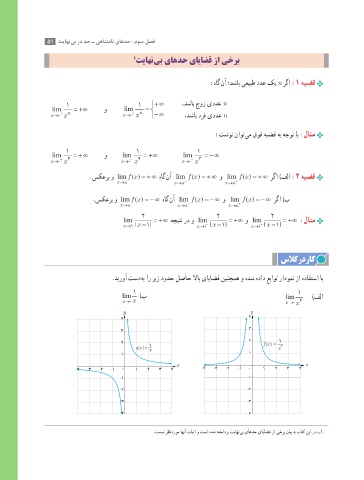
.دیروآ تسد هب ار ریز دودح لصاح لااب یایاضق نینچمه و هدش هداد عباوت رادومن زا هدافتسا اب
1 1
= +∞
lim )ب lim = +∞ )فلا
x→0 x x→0 x 2
y y
4
4
3 3

2 2 fx 1
() =
()=
g x 1 x x 2
1 1
x x
-4 -3 -2 -1 0 1 2 3 4 -4 -3 -2 -1 0 1 2 3 4
-1 -1
-2 -2

-3 -3
-4 -4

.تسین رظن دروم اهنآ تابثا و تسا هدش هتخادرپ تیاهن یب یاهدح یایاضق زا یخرب نایب هب باتک نیا رد ــ1