Page 63 - C112214

55 تیاهن یب رد دح ـ یهانتمان یاهدح : موس لصف

سلاکردراک

x
f
.دینک یسیونزاب lim ( ) = −∞ هک یتلاح رد ار ،5 هیضق 1
x→ a

.دیا هدرک هدافتسا هیضق مادک زا دینک صخشم هلحرم ره رد دیروآ تسد هب ار ریز دودح لصاح 2

2
x +1 x + x
فلا( lim ب( lim
x→1 − x −1 x→0 + x 2
x +2 2 − cos x
2
پ( lim ت( lim
x→−2 + x + 2 x + 4 4 x→0 − x

مئاق بناجم

1 1 1
() =
fx 1
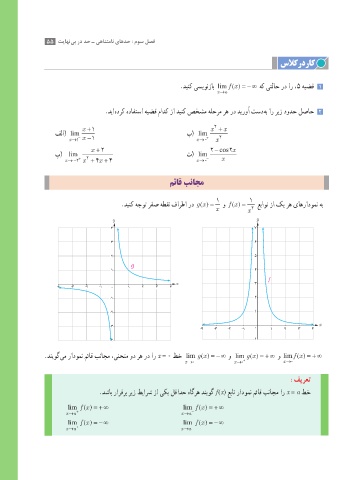
عباوت زا کی ره یاهرادومن هب
x .دینک هجوت رفص هطقن فارطا رد ()gx = و ()f x = ()fx =
x x 2 x 2
y y
4 7
3 6

2 5
g
1 4
f
x 3
-4 -3 -2 -1 0 1 2 3 4
-1 2

-2 1
-3 0 x
-4 -3 -2 -1 1 2 3 4
-4 -1

.دنیوگ یم رادومن مئاق بناجم ،ینحنم ود ره رد ار x = 0 طخ lim ( ) = −∞ و lim ( )gx = +∞ و lim ( ) = +∞
gx
f
x
x→0 − x→0 + x→0
:فیرعت
.دشاب رارقرب ریز طیارش زا یکی لقادح هاگره دنیوگ f (x) عبات رادومن مئاق بناجم ار x = a طخ

lim ( ) = +∞ lim ( ) = +∞
f
f
x
x
x→ a + x→ a −
lim ( ) = −∞ lim ( ) = −∞
f
x
f
x
x→ a + x→ a −