Page 64 - C112214

56

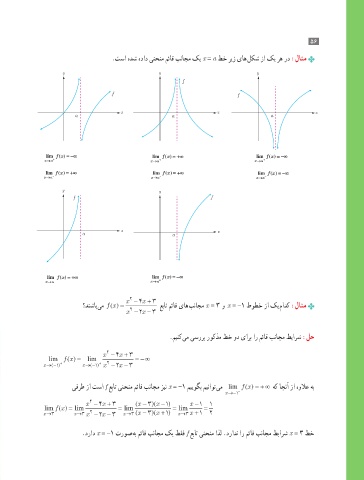
.تسا هدش هداد ینحنم مئاق بناجم کی x = a طخ ریز یاه لکش زا کی ره رد :لاثم

y y y
f
y y f y y f y y
f f
f f x x x
a a f f a

x x x x x x
a a a a a a

( )
lim fx = −∞ lim fx = +∞ lim fx = −∞
( )
( )
x→ a + x→ a + x→ a +
y
( )
y
( )
lim fx = +∞ lim fx = +∞ lim fx = −∞
( )
x→ a − f x→ a − f x→ a −
y y y y
f f f f
x x
a a
x x x x
a a a a

( )
( )
lim fx = +∞ lim fx = −∞
x→ a − x→ a +
x − 2 x +4 3
؟دنشاب یم ()f x = عبات مئاق یاه بناجم x = 3 و x = -1 طوطخ زا کی مادک :لاثم
x − 2 x −2 3

.مینک یم یسررب روکذم طخ ود یارب ار مئاق بناجم طیارش :لح

x − 2 x +4 3
( )
lim f x = lim = −∞
+
(
(
x→−1 ) + x→−1 ) x − 2 x −2 3
یفرط زا تسا f عبات ینحنم مئاق بناجم زین x = -1 مییوگب میناوت یم lim f ( ) = +∞ هک اجنآ زا هولاع هب
x
x →−1 −
x − 2 x +4 3 (x − )(x − 3 ) 1 x − 11
lim ( ) = lim = lim = lim =
x
f
x→ x→3 x 2 x −2 3 x→ − 3 (x − 3 )(x + 3 ) 1 x→ 3 x + 12
.دراد x = -1 تروص هب مئاق بناجم کی طقف f عبات ینحنم اذل .درادن ار مئاق بناجم طیارش x = 3 طخ