Page 67 - C112214

2 تیاهن یب رد دح

سرد

اب هک میدرک هدهاشم اجنآ رد میدرک یسررب ار ینحنم کی مئاق یاه بناجم و یهانتمان یاهدح لبق سرد رد
.دوش یم رت گرزب هاوخلد هب f (x) یددع هچ هب x ندش کیدزن
نیا ؟دنک یم یرییغت هچ f (x) ریداقم x )ندش کیدزن( ندش گرزب هاوخلد اب هک مینک یم یسررب سرد نیا رد

.تسا دیفم رایسب عبات رادومن یاه هخاش راتفر یسررب یارب و اهرادومن مسر رد بلطم

تیلاعف

y
4
1
x
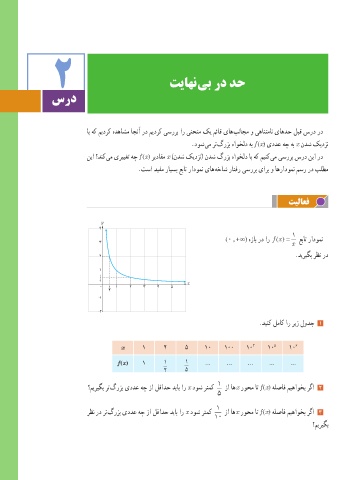
(0 , + ∞( هزاب رد ار () = عبات رادومن
f
3 x
2 .دیریگب رظن رد
1
1
2
1
3 x
0 1 1 2 3 4 5
2
-1
-2
.دینک لماک ار ریز لودج 1

x 1 2 5 1٠ 1٠٠ 1٠ 3 1٠ 5 1٠ 6

f (x) 1 1 1 … … … … …
2 5

1
؟میریگب رت گرزب یددع هچ زا لقادح دیاب ار x دوش رتمک زا اه x روحم ات f (x) هلصاف میهاوخب رگا 2
5
1
رظن رد رت گرزب یددع هچ زا لقادح دیاب ار x دوش رتمک زا اه x روحم ات f (x) هلصاف میهاوخب رگا 3
10
؟میریگب