Page 68 - C112214

60

1
؟میریگب رظن رد رت گرزب یددع هچ زا لقادح دیاب ار x دوش رت کچوک زا اه x روحم ات f (x) هلصاف میهاوخب رگا 4
100

؟داد شهاک هاوخلد نازیم ره هب ناوت یم ار اه x روحم ات f (x) هلصاف ایآ 5

1
دوش رایتخا گرزب یفاک هزادنا هب x هک یتروص رد درک هدهاشم ناوت یم لبق هحفص لودج و ()f x = عبات رادومن هب هجوت اب
ٔ x
دنک لیم تیاهن یب تبثم تمس هب x یتقو f (x) دح مییوگ یم تروص نیا رد .درک کیدزن رفص هب هاوخلد هزادنا هب ار f (x) ناوت یم
ٔ
1
lim =0 .میسیون یم و تسا رفص ربارب
x→+ ∞ x

سلاکردراک
1
() =
fx
x
y
1
1
f
x
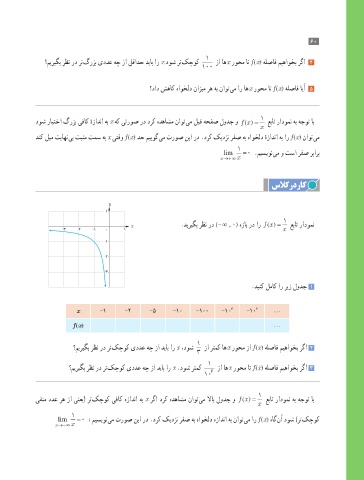
x .دیریگب رظن رد (- ∞ , 0) هزاب رد ار () = عبات رادومن
-3 -2 -1 0 1 x
-1

-2

-3

.دینک لماک ار ریز لودج 1

x -1 -2 -5 -1٠ -1٠٠ -1٠ 3 -1٠ 4 ...

f (x) ...

1
؟میریگب رظن رد رت کچوک یددع هچ زا دیاب ار x ،دوش زا رتمک اه x روحم زا f (x) هلصاف میهاوخب رگا 2
3
1
؟میریگب رظن رد رت کچوک یددع هچ زا دیاب ار x .دوش رتمک زا اه x روحم ات f (x) هلصاف میهاوخب رگا 3
10 6

1
یفنم ددع ره زا ینعی( رت کچوک یفاک هزادنا هب x رگا درک هدهاشم ناوت یم لااب لودج و () = عبات رادومن هب هجوت اب
x
f
x
1
lim =0 :میسیون یم تروص نیا رد .درک کیدزن رفص هب هاوخلد هزادنا هب ناوت یم ار f (x) هاگ نآ دوش )رت کچوک
x→−∞ x