Page 69 - C112214

61 تیاهن یب رد دح ـ یهانتمان یاهدح : موس لصف

روط هب لبق هحفص سلاک رد راک و تیلاعف هب هجوت اب اذل x → - ∞ ای x → + ∞ هک تسا نآ x → ± ∞ زا روظنم :رکذت
ٔ
:تشون ناوت یم هصلاخ

1
lim =0
x→±∞ x

:فیرعت
دنک یم لیم تیاهن یب تبثم تمس هب x یتقو f (x) دح مییوگ دشاب هدش فیرعت (a , + ∞( دننام یا هزاب رد f (x) عبات رگا

ره هب ار l زا f (x) هلصاف ،گرزب یفاک ردق هب یاه x رایتخا اب ناوتب هاگره lim f ( ) =l میسیون یم و تسا l ربارب
x
x →+∞
.درک کچوک هزادنا
l ربارب دنک یم لیم تیاهن یب یفنم تمس هب x یتقو f (x) دح مییوگ یم .دشاب هدش فیرعت (- ∞ , a) هزاب رد f عبات رگا

هزادنا ره هب l زا ار f (x) هلصاف کچوک یفاک ردق هب یاه x رایتخا اب ناوتب هاگره lim f ( ) =l میسیون یم و تسا
x
x →− ∞
.درک کچوک

سلاکردراک

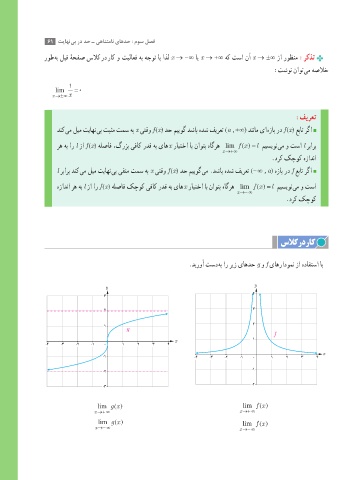
.دیروآ تسد هب ار ریز یاهدح g و f یاهرادومن زا هدافتسا اب
() =
fx 1
x 2
y y
4
3
2 3

2
1
g
f
x 1
-4 -3 -2 -1 0 1 2 3 4
x
-1 -4 -3 -2 -1 0 1 2 3 4
-1
-2
-2
-3

( )
lim gx = lim f ( ) =
x
x→+ ∞ x→+ ∞
lim gx = lim f ( ) =
( )
x
x→− ∞ x→− ∞