Page 71 - C112214

63 تیاهن یب رد دح ـ یهانتمان یاهدح : موس لصف

تیاهن یب رد یهانتمان یاهدح

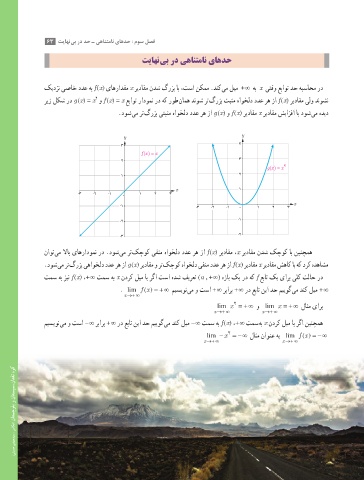
کیدزن یصاخ ددع هب f (x) یاهرادقم x ریداقم ندش گرزب اب ،تسا نکمم .دنک یم لیم + ∞ هب x یتقو عباوت دح هبساحم رد
2
ریز لکش رد g (x) = x و f (x) = x عباوت رادومن رد هک روط نامه دنوش رت گرزب تبثم هاوخلد ددع ره زا f (x) ریداقم یلو دنوشن
.دوش یم رت گرزب یتبثم هاوخلد ددع ره زا g (x) و f (x) ریداقم x ریداقم شیازفا اب دوش یم هدید

y y
3 4
() =
fx x
2 3
() =
gx x 2
1 2
x 1
-3 -2 -1 1 2 3
0
x
-1 -3 -2 -1 0 1 2 3
-1
-2
-2
-3

ناوت یم لااب یاهرادومن رد .دوش یم رت کچوک یفنم هاوخلد ددع ره زا f (x) ریداقم ،x ریداقم ندش کچوک اب نینچمه
.دوش یم رت گرزب یهاوخلد ددع ره زا g (x) ریداقم و رت کچوک هاوخلد یفنم ددع ره زا f (x) ریداقم x ریداقم شهاک اب هک درک هدهاشم
تمس هب زین f (x) ،+ ∞ تمس هب x ندرک لیم اب رگا تسا هدش فیرعت (a , + ∞( هزاب کی رد هک f عبات کی یارب یلک تلاح رد

. lim f ( ) = +∞ میسیون یم و تسا + ∞ ربارب + ∞ رد عبات نیا دح مییوگ یم دنک لیم + ∞
x
x→+ ∞
2
lim x = +∞ و lim x = +∞ لاثم یارب
x→+ ∞ x→+ ∞
میسیون یم و تسا - ∞ ربارب + ∞ رد عبات نیا دح مییوگ یم دنک لیم - ∞ تمس هب f (x) ،+ ∞ تمس هب x ندرک لیم اب رگا نینچمه
2
lim − x = −∞ لاثم ناونع هب lim f ( ) = −∞
x
x→+ ∞ x→+ ∞

)ینیسح یدهمدیس :ساکع( ناتسچولب و ناتسیس،ناتفت هوک