Page 75 - C112214

67 تیاهن یب رد دح ـ یهانتمان یاهدح : موس لصف

یقفا بناجم

=
x
و lim f ( ) L طرش ود زا یکی لقادح هک یطرش هب میمان یم y = f (x) رادومن یقفا بناجم ار y = L طخ
x→+ ∞
=
x
دشاب رارقرب lim f ( ) L
x→− ∞
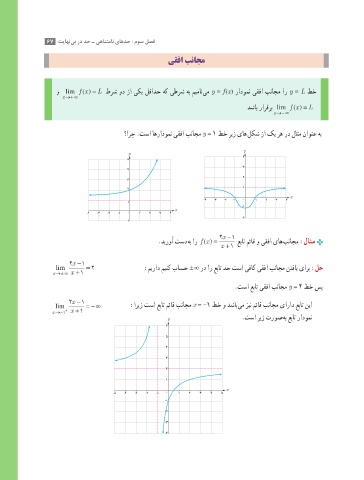
؟ارچ .تسا اهرادومن یقفا بناجم y = 1 طخ ریز یاه لکش زا کی ره رد لاثم ناونع هب

y
y
4
5
3
4
2
3
1
2
x
-4 -3 -2 -1 0 1 2 3 4
1
-1
x
-4 -3 -2 -1 0 1 2 3 4
-2
-1
2 x −1
.دیروآ تسد هب ار ()f x = عبات مئاق و یقفا یاه بناجم :لاثم
x +1
2 x −1
lim = 2 :میراد مینک باسح ± ∞ رد ار عبات دح تسا یفاک یقفا بناجم نتفای یارب :لح
x→± ∞ x +1
.تسا عبات یقفا بناجم y = 2 طخ سپ

x 2 −1
lim = −∞ :اریز تسا عبات مئاق بناجم x = -1 طخ و دشاب یم زین مئاق بناجم یاراد عبات نیا
x →−1 + x +1
y .تسا ریز تروص هب عبات رادومن
6

5
4
3
2
1
x
-5 -4 -3 -2 -1 0 1 2 3 4 5
-1
-2
-3
-4