Page 82 - C112214

74

تیلاعف

ینحنم یور ار A تباث هطقن .مینک یسررب ار هطقن کی رد ینحنم رب سامم طخ ،ینحنم رادومن کمک هب هک مینک یم یعس نونکا
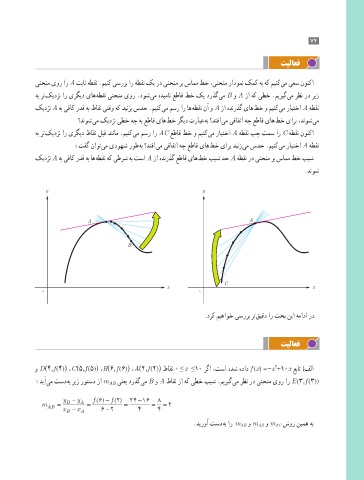
هب رت کیدزن ار یرگید یاه هطقن ینحنم یور .دوش یم هدیمان عطاق طخ کی درذگ یم B و A زا هک یطخ .میریگ یم رظن رد ریز

کیدزن A هب یفاک ردق هب طاقن یتقو هک دینزب سدح .مینک یم مسر ار اه هطقن نآ و A زا هدنرذگ یاه طخ و مینک یم رایتخا A هطقن
؟دنوش یم کیدزن یطخ هچ هب عطاق یاه طخ رگید ترابع هب ؟دتفا یم یقافتا هچ عطاق یاه طخ یارب ،دنوش یم

هب رت کیدزن ار یرگید طاقن لبق دننام .مینک یم مسر ار AC عطاق طخ و مینک یم رایتخا A هطقن پچ تمس ار C هطقن نونکا
:تفگ ناوت یم یدوهش روط هب ؟دتفا یم یقافتا هچ عطاق یاه طخ یارب دینز یم سدح .مینک یم رایتخا A هطقن

کیدزن A هب یفاک ردق هب اه هطقن هک یطرش هب تسا A زا هدنرذگ عطاق یاه طخ بیش دح A هطقن رد ینحنم رب سامم طخ بیش
.دنوش

y y

A A

B

C
x x
0 0

.درک میهاوخ یسررب رت قیقد ار ثحب نیا همادا رد

تیلاعف

2

و D (4, f (4)) ،C (5, f (5)) ،B(6, f (6)) ،A(2, f (2)) طاقن 0 ≥ x ≥10 رگا ،تسا هدش هداد f (x) = - x +10x عبات )فلا
:دیآ یم تسد هب ریز روتسد زا m ینعی درذگ یم B و A طاقن زا هک یطخ بیش .میریگ یم رظن رد ینحنم یور ار E (3, f (3))
AB
− f
y − f ( ) −y 6 () 2 24 16 8
m AB = x B − A = 6 2 = 4 = 4 = 2
−x
B
A
.دیروآ تسد هب ار m AE و m AD و m AC شور نیمه هب