Page 87 - C112214

79 قتشم : مراهچ لصف
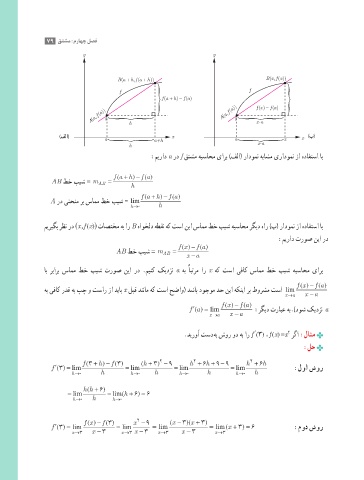
y y

( , ( ))
B (a + h ,(a + f h)) Bx f x
f f
( fa + ) h − fa
()
x
()
(a)) (a , f (a)) f ( ) − fa
, f
A (a h A x-a
)فلا( x x )ب(
a a+h a x
h x-a
:میراد a رد f قتشم هبساحم یارب )فلا( رادومن هباشم یرادومن زا هدافتسا اب

+
( fa h − ) fa
()
AB طخ بیش = m AB = h
()
−
+
( fa h ) fa
A رد ینحنم رب سامم طخ بیش = lim
h→0 h
میریگب رظن رد (x , f (x)) تاصتخم هب ار B هاوخلد هطقن هک تسا نیا سامم طخ بیش هبساحم رگید هار )ب( رادومن زا هدافتسا اب

:میراد تروص نیا رد
−
()
f ( ) fa
x
AB طخ بیش = m AB = xa
−
اب ربارب سامم طخ بیش تروص نیا رد .مینک کیدزن a هب ًابترم ار x هک تسا یفاک سامم طخ بیش هبساحم یارب
()
−
f ( ) fa
x
هب یفاک ردق هب پچ و تسار زا دیاب x لبق دننام هک تسا حضاو( دشاب دوجوم دح نیا هکنیا رب طورشم تسا lim
−
x→ a xa
()
x
f ( ) − fa
( ) =
′ fa lim :رگید ترابع هب.)دوش کیدزن a
−
x →a xa
′
2
.دیروآ تسد هب شور ود هب ار f (3) ، f (x) =x رگا :لاثم
:لح
3
f ′ ( ) lim ( f 3 + ) h − f ( ) = lim (h + 3 ) − 2 = lim h +9 2 6 h + 9 − = lim h +9 2 h 6 :لوا شور
=
3
→
→
h 0 h h 0 h h 0 h h 0 h
→
→
( hh +6 )
= lim = lim(h + ) =6 6
→
→
h 0 h h 0
−
x
3
f () f ( ) x − 2 9 (x − )(x + 3 ) 3
( ) =
f ′ 3 lim = lim = lim = lim(x + ) = 3 6 :مود شور
x→ x − x→3 3 x − 3 3 x→ x − 3 x→3 3