Page 92 - C112214

2

یگتسویپ و یریذپ قتشم

سرد

:دش فیرعت ریز تروص ود زا یکی هب x لوط هب یا هطقن رد f عبات قتشم هتشذگ سرد رد
0
x
( + f x ) −h f () f () − f ( )
x
x
( ) lim
′
( ) =
′ fx 0 = 0 0 ای fx 0 lim 0
−
h →0 h x →x 0 xx 0
.تسا ریذپ قتشم x رد f هک دوش یم هتفگ قوف )یهانتم( دح دوجو تروص رد
0
.تسا تیمها یاراد تسین ریذپ قتشم طاقن نآ رد عبات هک یطاقن ندرک صخشم ،عبات کی راتفر هعلاطم رد
.دیوش یم انشآ تسین ریذپ قتشم نآ رد عبات کی هک ییاه تلاح زا یکی اب ریز تیلاعف رد
تیلاعف

 x 2 x ≠ 2
f x
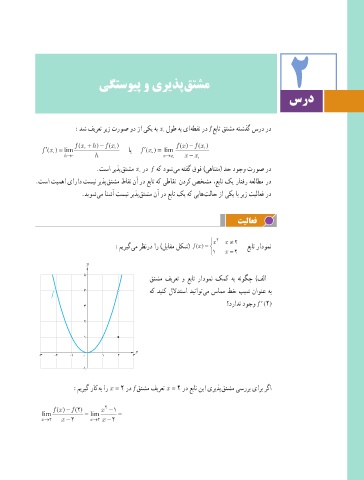
:میریگ یم رظنرد ار )لباقم لکش( () =  عبات رادومن
  1 x = 2
y
5
قتشم فیرعت و عبات رادومن کمک هب هنوگچ )فلا

f 4 هک دینک للادتسا دیناوت یم سامم طخ بیش ناونع هب
؟درادن دوجو f ′ (2)
3

2

1

x
-3 -2 -1 0 1 2 3
-1

:میریگ راک هب ار x = 2 رد f قتشم فیرعت x = 2 رد عبات نیا یریذپ قتشم یسررب یارب رگا

( ) −
2
f x () x 2 − f 1
lim = lim =
−2
x → x − x →2 2 x 2