Page 93 - C112214

85 قتشم : مراهچ لصف

:میراد ،x →2 یتقو .تسا رفص ربارب رسک جرخم دح و تسا 3 ربارب رسک تروص دح

x 2 −1
تسار دح = lim = +∞
+
x →2 x −2
x 2 −1
پچ دح = lim = −∞
−
x →2 x −2
f ( ) − f ()
2
x
.درادن دوجو f ′ (2) سپ ،تسین )یهانتم و( دوجوم lim نیاربانب
x →2 x −2
هسیاقم ناتناتسود خساپ اب ار دوخ خساپ ؟تسا ریذپ قتشم هطقن نیا رد عبات ایآ .دیریگب رظن رد )x = 2 زج هب( یرگید هطقن )ب

.دینک

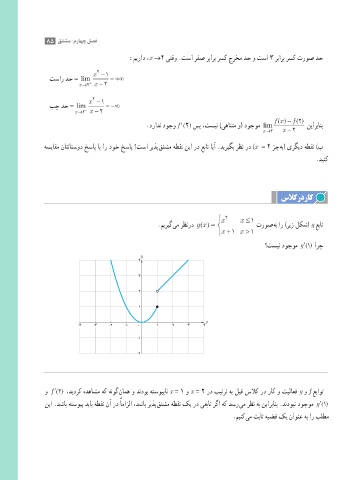
سلاکردراک

 2 x ≤1
x
.میریگ یم رظنرد () =gx  تروص هب ار )ریز لکش( g عبات
x +   x 1
>1
؟تسین دوجوم ()1g ′ ارچ
y
4

3

2

1

x
-4 -3 -2 -1 0 1 2 3 4
-1

-2

و ()2f ′ ،دیدرک هدهاشم هک هنوگ نامه و دندوب هتسویپان x = 1 و x = 2 رد بیترت هب لبق سلاک رد راک و تیلاعف g و f عباوت

نیا .دشاب هتسویپ دیاب هطقن نآ رد ًامازلا ،دشاب ریذپ قتشم هطقن کی رد یعبات رگا هک دسر یم رظن هب نیاربانب .دندوبن دوجوم ()1g ′
.مینک یم تباث هیضق کی ناونع هب ار بلطم