Page 94 - C112214

86

.تسا هتسویپ a رد f هاگ نآ دشاب ریذپ قتشم x = a رد f عبات رگا :هیضق

( )
x
f
lim ( ) = fa :میهد ناشن تسا یفاک :تابثا
x →a
()
x
f ( ) − fa
lim( ( ) − f x ( )) = fa lim(( − x a )( )) =
−
x → x →a a xa
()
f ( ) − fa
x
lim( − x ).lim( ) =a 0 . ( ) = ′ fa 0
−
x → x →a a xa
)؟ارچ( lim ( ) =f x fa ( )) = fa 0 نیاربانب
( ) اجنآ زا و lim( ( ) − f x
x →a x →a
:هک تفرگ هجیتن ناوت یم یقطنم روط هب هیضق نیا هب هجوت اب
.تسین مه ریذپ قتشم x = a رد f هاگ نآ ،دشابن هتسویپ x = a رد f عبات رگا

یریذپ قتشم ناوت یمن ًاموزل ،هطقن کی رد عبات یگتسویپ دوجو اب یتح ینعی ،تسین تسرد هیضق سکع هک دهد یم ناشن دعب لاثم

.تفرگ هجیتن ار هطقن نآ رد عبات
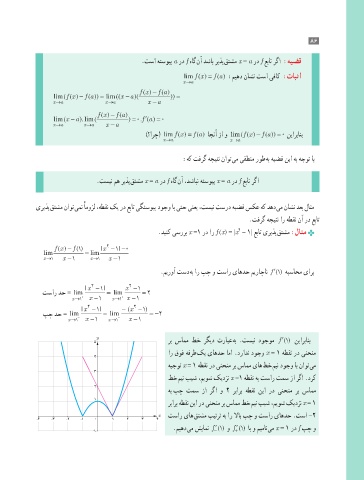
2
.دینک یسررب x =1 رد ار f (x) = |x - 1| عبات یریذپ قتشم :لاثم
|
x
f ( ) − f () |x 2 −−10
1
lim = lim
−1
x → x − x →1 1 x 1
.میروآ تسد هب ار پچ و تسار یاهدح میراچان ()1f ′ هبساحم یارب
|x 2 − | x 2 −1 1
تسار دح = lim = lim = 2
+
x → + − x →1 x 1 x −1 1
|x − 2 | 1 − (x − 2 ) 1
lim
پچ دح = lim fx x −1 = −2
() = =
2
x→ − x − x→1 1 − x −1 1
y ′
1
f
5 رب سامم طخ رگید ترابع هب .تسین دوجوم () نیاربانب
ار قوف هفرط کی یاهدح اما .درادن دوجو x = 1 هطقن رد ینحنم
4
هیجوت x = 1 هطقن رد ینحنم رب سامم یاه طخ مین دوجو اب ناوت یم
3
طخ مین بیش ،میوش کیدزن x =1 هطقن هب تسار تمس زا رگا .درک
2
هب پچ تمس زا رگا و 2 ربارب هطقن نیا رد ینحنم رب سامم
1
ربارب هطقن نیا رد ینحنم رب سامم طخ مین بیش ،میوش کیدزن x = 1
x تسار یاه قتشم بیترت هب ار لااب پچ و تسار یاهدح .تسا -2
-4 -3 -2 -1 0 1 2 3 4
1
.میهد یم شیامن ′ f () و ′ f () اب و میمان یم x = 1 رد f پچ و
1
-1 − +