Page 96 - C112214

88

′
′
gx
g
0
0
f
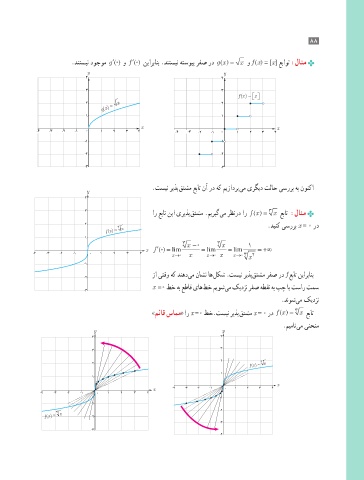
.دنتسین دوجوم () و () نیاربانب .دنتسین هتسویپ رفص رد () = x و f (x) = [x] عباوت :لاثم
y y
4 4
3 3
x 
() =
fx 
2 x 2
g x ( ) =
1 1
x x
-4 -3 -2 -1 0 1 2 3 4 -4 -3 -2 -1 0 1 2 3 4
-1 -1
-2 -2
-3 -3

.تسین ریذپ قتشم عبات نآ رد هک میزادرپ یم یرگید تلاح یسررب هب نونکا
y
4

ار عبات نیا یریذپ قتشم .میریگ یم رظنرد ار () =f x x عبات :لاثم
3 3
2 3 .دینک یسررب x = 0 رد
f ( ) x = x
1
3 x −0 3 x 1
=
0
x ′ f ( ) lim = lim = lim = +∞
-4 -3 -2 -1 0 1 2 3 4 x 0 x 0 x 0 3 x 2
→ x
→ x
→
-1
زا یتقو هک دنهد یم ناشن اه لکش .تسین ریذپ قتشم رفص رد f عبات نیاربانب
-2
x =0 طخ هب عطاق یاه طخ میوش یم کیدزن رفص هطقن هب پچ ای تسار تمس
-3
.دنوش یم کیدزن
»مئاق سامم« ار x =0 طخ.تسین ریذپ قتشم x = 0 رد () =f x 3 x عبات
.میمان یم ینحنم
y y
4 4
3
3
2 3
2 ( ) x = x
f
1
1
x
x -4 -3 -2 -1 0 1 2 3 4
-4 -3 -2 -1 0 1 2 3 4
-1
-1
f ( ) x = 3 x -2 -2
-3
-3
-2