Page 98 - C112214

90

قتشم عبات

کی هنماد هب قلعتم طاقن هعومجم نیب یا هطبار نتفای لابند هب لاح .دیا هدش انشآ )نیعم( هطقن کی رد عبات قتشم موهفم اب نونکات
.میتسه طاقن نآ رد عبات قتشم و عبات

تیلاعف

y
4

3 2
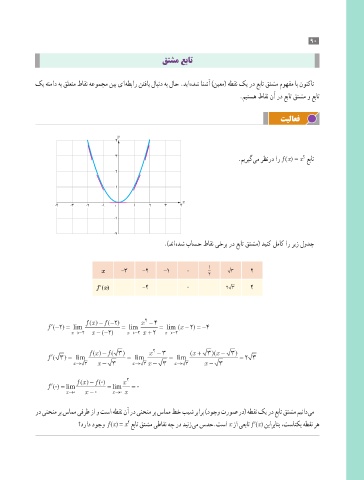
.میریگ یم رظنرد ار f )x) = x عبات
2

1

x
-4 -3 -2 -1 0 1 2 3 4
-1

-2
.)دنا هدش باسح طاقن یخرب رد عبات قتشم( دینک لماک ار ریز لودج

1
x -3 -2 -1 0 3 2
2
f ′ (x) -4 0 2 3 4

() − f x ( 2 ) 2 −x 4
− f
( ′ −f ) =2 lim = lim = lim ( − x ) =2 − 4
x →−2 x − (−2 ) x →−2 x +2 x →−2

( ) − f x f ( 3 ) x 2 − 3 ( + x )( − 3 x ) 3
( ′ f 3 ) = lim = lim = lim = 23
x → 3 x x → − − 3 x → 3 x 3 x −3 3

x
0
=
′ f ( ) lim f ( ) − f () = lim x 2 =0
0
x → x −0 x →0 0 x
رد ینحنم رب سامم یفرط زا و تسا هطقن نآ رد ینحنم رب سامم طخ بیش ربارب )دوجو تروص رد( هطقن کی رد عبات قتشم میناد یم

2
؟دراد دوجو f )x) = x عبات قتشم یطاقن هچ رد دینز یم سدح.تسا x زا یعبات f ′)x) نیاربانب ،تساتکی هطقن ره