Page 99 - C112214

91 قتشم : مراهچ لصف

:مینک یم فیرعت ریز تروص هب ار نآ و میهد یم شیامن f ′)x) اب ار x رد f قتشم عبات ،دشاب f عبات هنماد زا یوضع x رگا

( + f x h ) − f ()
x
( ) lim
′ fx =
h →0 h
.میمان یم f ′ هنماد ار دشاب دوجوم f ′ اهنآ یارب هک f هنماد زا یطاقن مامت هعومجم .دشاب دوجوم قوف دح هکنآ رب طورشم

2
هئارا همادا رد ،زین f ′ عبات هطباض هبساحم شور .تسا یقیقح دادعا هعومجم ،f ′ عبات هنماد ، f )x) = x عبات یارب لاثم روط هب
.تسا هدش

x
( + f x h ) − f ( ) ( + x h ) − 2 x 2
( ) lim
′ fx = = lim
h → h h →0 0 h
2 + x + 2hxh 2 − x 2 (2xh )
+ h
+
= lim = lim = lim(2xh ) = 2x
h → 0 h → h h h →0 0
قتشم رادقم روتسد نیا کمک هب .تسا یقیقح دادعا هعومجم ،f ′ عبات هنماد دش رکذ لابق هک هنوگ نامه .f ′)x) =2 x نیاربانب
ً
2
:لاثم روط هب ،درک باسح ناوت یم ار هطقن ره رد f (x) = x عبات

1 2
f
( ′ − f ) = − , ( ′ 7 ) = 2 7 و f ′)50) = 100
5 5

1
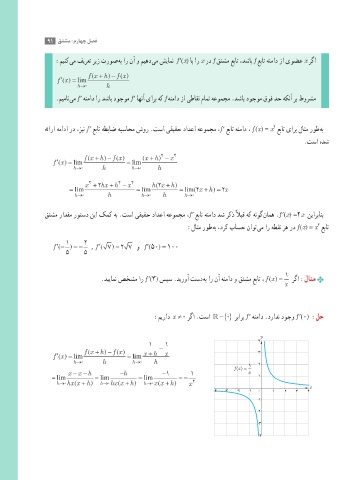
.دییامن صخشم ار f ′)3) سپس .دیروآ تسد هب ار نآ هنماد و قتشم عبات ، () =f x رگا :لاثم
x

:میراد ≠0 رگا .تسا  − { } 0 ربارب f ′ هنماد .درادن دوجو f ′)0) :لح
x

y
1 1 4
( + f x h ) − f () xh − x 3
x
+
( ) lim
′ fx = = lim
h → h h 0 h 1 2
→0
() =
fx
x −−xh −h −1 1 x
= lim = lim = lim = − 1
( +
h → ( + ) h h →0hxx ( + ) h h →0hxx 0xx ) h x 2
-4 -3 -2 -1 0 1 2 3 4 x
-1
-2
-3
-4