Page 100 - C112211

قتشم 4 لصف

مود هبترم قتشم

مود هبترم قتشم ،دشاب ریذپ قتشم ،قتشم عبات رگا بیترت نیمه هب .دش هداد شیامن y′ = f ′)x( دامن اب y = f )x( عبات قتشم
.میریگ یم قتشم x هب تبسن y′ = f ′)x( عبات زا نآ هبساحم یارب و میهد یم شیامن y″ = f ″)x( هب ار y = f )x(

2
4
:هاگ نآ y = 3x + 2x -1 رگا :لاثم
2
3
y′ = 12x + 4x , y″ = 36x + 4
نیرتم

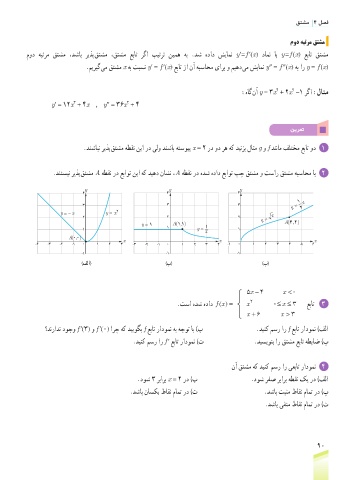
.دنشابن ریذپ قتشم هطقن نیا رد یلو دنشاب هتسویپ x = 2 رد ود ره هک دینزب لاثم g و f دننام فلتخم عبات ود 1

.دنتسین ریذپ قتشم A هطقن رد عباوت نیا هک دیهد ناشن ،A هطقن رد هدش هداد عباوت پچ قتشم و تسار قتشم هبساحم اب 2

y y y
4 4 4
1 x
3 3 3 y = 2
y = − x y = x 2 x
2 2 2 y =
42
11
y = 1 A (, ) A (, )
1 1 y = 1 1
x
A (, )
00
-4 -3 -2 -1 0 1 2 3 x -3 -2 -1 0 1 2 3 4 x -1 0 1 2 3 4 5 6 x
-1 -1 -1
)فلا( )ب( )پ(

5 x −4 x <0

.تسا هدش هداد )(f x = x 2 0 ≤≤ 3 عبات 3
x
x +6 x > 3

؟دنرادن دوجو f ′)3( و f ′)0( ارچ هک دییوگب f عبات رادومن هب هجوت اب )ب .دینک مسر ار f عبات رادومن )فلا
.دینک مسر ار f ′ عبات رادومن )ت .دیسیونب ار قتشم عبات هطباض )پ

نآ قتشم هک دینک مسر ار یعبات رادومن 4

.دوش 3 ربارب x = 2 رد )ب .دوش رفص ربارب هطقن کی رد )فلا
.دشاب ناسکی طاقن مامت رد )ت .دشاب تبثم طاقن مامت رد )پ

.دشاب یفنم طاقن مامت رد )ث

90