Page 117 - C112211

عبات یاه ممرتسکا لوا سرد

سلاک رد راک

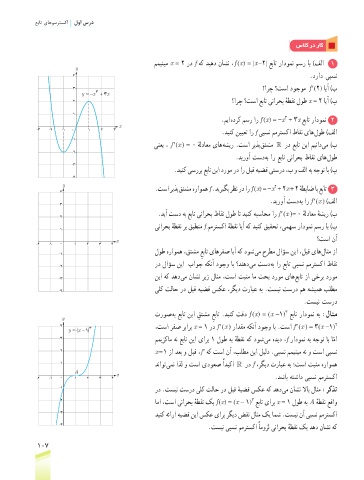
ممینیم x = 2 رد f هک دیهد ناشن ، f )x( = |x -2| عبات رادومن مسر اب )فلا 1
y
4 .دراد یبسن
3 ؟ارچ ؟تسا دوجوم f ′ )2( ایآ )ب
y = x − 3 + 3 x
2 ؟ارچ ؟تسا عبات ینارحب هطقن لوط x = 2 ایآ )پ
ٔ
1
3
.میا هدرک مسر ار f )x( = -x + 3x عبات رادومن 2
x
-3 -2 -1 0 1 2 3
.دینک نییعت ار f یبسن ممرتسکا طاقن یاه لوط )فلا
-1
ینعی ، f ′ )x ( = 0 هلداعم یاه هشیر .تسا ریذپ قتشم  رد عبات نیا میناد یم )ب
ٔ
-2
.دیروآ تسد هب ار عبات ینارحب طاقن یاه لوط
-3
.دینک یسررب عبات نیا دروم رد ار لبق هیضق یتسرد ،ب و فلا هب هجوت اب )پ
-4
y 2
ٔ
4 .تسا ریذپ قتشم هراومه f .دیریگب رظن رد ار f )x( = -x + 2x + 2 هطباض اب عبات ٣
.دیروآ تسد هب ار f ′ )x ( )فلا
3
.دیآ تسد هب عبات ینارحب طاقن لوط ات دینک هبساحم ار f ′ )x (= 0 هلداعم هشیر )ب
2 ٔ ٔ
ینارحب هطقن رب قبطنم f ممرتسکا هطقن ایآ هک دینک قیقحت ،یمهس رادومن مسر اب )پ
1 ٔ ٔ
x ؟تسا نآ
-2 -1 0 1 2 3 4
لوط هراومه ،قتشم ِ عبات یاهرفص ایآ هک دوش یم حرطم لاؤس نیا ،لبق یاه لاثم زا
-1
رد لاؤس نیا باوج هکنآ دوجو اب ؟دنهد یم تسد هب ار عبات یبسن ممرتسکا طاقن
-2
نیا هک دهد یم ناشن ریز لاثم ،تسا تبثم ام ثحب دروم یاه عبات زا یخرب دروم
-3
یلک تلاح رد لبق هیضق سکع ،رگید ترابع هب .تسین تسرد مه هشیمه بلطم
-4
.تسین تسرد

ِ
3
تروص هب عبات نیا قتشم ِ عبات .دینک تقد f )x( = )x -1( عبات رادومن هب :لاثم
y
4 ،تسا رفص ربارب x = 1 رد f ′ )x ( رادقم هکنآ دوجو اب .تسا f ′ )x ( = 3)x -1( 2
y = (x −1 ) 3
3 ممیزکام هن عبات نیا یارب 1 لوط هب هطقن هک دوش یم هدید ،f رادومن هب هجوت اب اما
ٔ
ّ
2 x = 1 زا دعب و لبق ،f ′ هک تسا نآ ،بلطم نیا لیلد .یبسن ممینیم هن و تسا یبسن
1 دناوت یمن اذل و تسا یدوعص ًادیکا  رد f ،رگید ترابع هب ؛تسا تبثم هراومه
A
-2 -1 0 1 2 3 4 x .دشاب هتشاد یبسن ممرتسکا
-1 رد .تسین تسرد یلک تلاح رد لبق هیضق سکع هک دهد یم ناشن لااب لاثم :رکذت
ٔ
-2 3
اما ،تسا ینارحب هطقن کی f )x( = )x - 1( عبات یارب x = 1 لوط هب A هطقن عقاو
ٔ
ٔ
-3
دینک هئارا هیضق نیا سکع یارب رگید ضقن لاثم کی امش .تسین نآ یبسن ممرتسکا
-4
.تسین یبسن ممرتسکا ًاموزل ینارحب هطقن کی دهد ناشن هک
ٔ
107