Page 121 - C112211

عبات یاه ممرتسکا لوا سرد

تیلاعف

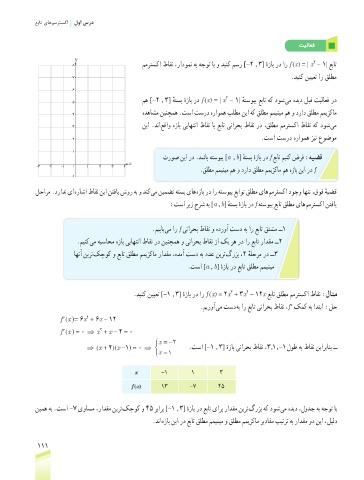
y
2
8 ممرتسکا طاقن ،رادومن هب هجوت اب و دینک مسر [-2 , 3] هزاب رد ار f )x) = | x - 1| عبات
ٔ
7 .دینک نییعت ار قلطم
6
2
مه [-2 , 3] هتسب هزاب رد f )x) = | x - 1| هتسویپ عبات هک دوش یم هدید لبق تیلاعف رد
5 ٔ ٔ ٔ
هدهاشم نینچمه .تسا تسرد هراومه بلطم نیا هک قلطم ممینیم مه و دراد قلطم ممیزکام
4
3 نیا .دنا عقاو هزاب ییاهتنا طاقن ای عبات ینارحب طاقن رد ،قلطم ممرتسکا طاقن هک دوش یم
2 .تسا تسرد هراومه زین عوضوم

1
تروص نیا رد .دشاب هتسویپ [a , b] هتسب هزاب رد f عبات مینک ضرف :هیضق
ٔ
ٔ
x
-3 -2 -1 0 1 2 3 4
.قلطم ممینیم مه و دراد قلطم ممیزکام مه هزاب نیا رد f
-1
لحارم .درادن یا هراشا طاقن نیا نتفای شور هب و دنک یم نیمضت هتسب یاه هزاب رد ار هتسویپ عباوت قلطم یاه ممرتسکا دوجو اهنت ،قوف هیضق
ٔ
:تسا ریز حرش هب [a , b] هتسب هزاب رد f هتسویپ عبات قلطم یاه ممرتسکا نتفای
ٔ
ٔ

.میبای یم ار f ینارحب طاقن و هدروآ تسد هب ار عبات قتشم ــ1
.مینک یم هبساحم هزاب ییاهتنا طاقن رد نینچمه و ینارحب طاقن زا کی ره رد ار عبات رادقم ــ2

اهنآ نیرت کچوک و عبات قلطم ممیزکام رادقم ،هدمآ تسد هب ددع نیرت گرزب ،2 هلحرم رد ــ3
ٔ
.تسا [a , b] هزاب رد عبات قلطم ممینیم
ٔ

2
3
.دینک نییعت [-1 , 3] هزاب رد ار f )x) = 2x + 3x - 12x عبات قلطم ممرتسکا طاقن :لاثم
ٔ
.میروآ یم تسد هب ار عبات ینارحب طاقن ،f ′ کمک هب ادتبا :لح
2
f ′ (x (= 6x + 6x - 12
2
f ′ (x ( = 0 ⇒ x + x - 2 = 0
x = −2
⇒ (x + 2)(x -1) = 0 ⇒  .تسا [-1 , 3] هزاب ینارحب طاقن ،٣,1 , -1 لوط هب طاقن نیاربانب ــ
ٔ
 x =1

x -1 1 3
f )x( 13 -7 45

نیمه هب .تسا -7 یواسم ،رادقم نیرت کچوک و 45 ربارب [-1 , 3] هزاب رد عبات یارب رادقم نیرت گرزب هک دوش یم هدید ،لودج هب هجوت اب
ٔ
.دنا هزاب نیا رد عبات قلطم ممینیم و قلطم ممیزکام ریداقم بیترت هب رادقم ود نیا ،لیلد

111