Page 124 - C112211

قتشم دربراک 5 لصف

l ار تحاسم نیرتشیب یلیطتسم ،رتم یتناس 14 تباث طیحم اب یاه لیطتسم مامت نیب رد دیهد ناشن :١ لاثم

.دنشاب هزادنا مه نآ ضرع و لوط هک دراد
x
:تسا لیطتسم تحاسم ،دوش ممیزکام تسا رارق هک یتیمک .دنشاب l و x لیطتسم داعبا مینک ضرف :لح
S = x.l )1(
:میروآ تسد هب x بسحرب ار l میناوت یم ،دوش نایب x زا یعبات تروص هب S هکنآ یارب

لیطتسم طیحم :P = 14
٢)x + l ( = 14 ⇒ x + l = 7 ⇒ l = 7 - x )٢(

:تشاد میهاوخ )1( رد )2( هطبار یراذگیاج اب
S )x( = x )7 - x(
S )x( = -x + 7x , x ∈ [0,7]
2
.میبایب ار S ′(x( = 0 هلداعم هشیر تسا یفاک نآ ینارحب طاقن نتفای یارب نیاربانب ،تسا ریذپ قتشم )٠,٧( هزاب رد S
ٔ
ٔ
ٔ
S ′(x( = 0 ⇒ -2x + 7 = 0 ⇒ x = 3/5 .تسا [0,7] هزاب ینارحب طاقن ،٠,٧ , 3/5 لوط هب طاقن نیاربانب
ٔ
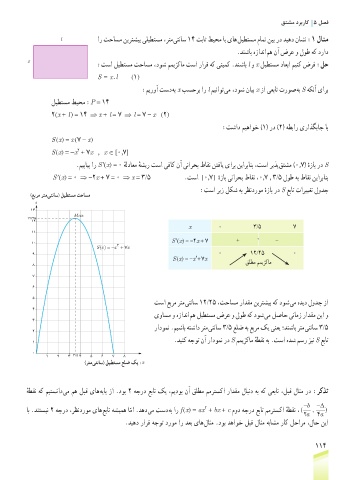
:تسا ریز لکش هب رظندروم هزاب رد S عبات تارییغت لودج
)عبرم رتم یتناس( لیطتسم تحاسم ٔ
s
13
Max
12/25
12
x 0 3/5 7
11
S ′(x( = -2x + 7 + 0 -
10 2
() =
Sx x − + 7 x
9 0 12/25 0
S )x( = -x + 7x
2
8 قلطم ممیزکام
7
6
5
تسا عبرم رتم یتناس 12/25 ،تحاسم رادقم نیرتشیب هک دوش یم هدید لودج زا
4
یواسم و هزادنا مه لیطتسم ضرع و لوط هک دوش یم لصاح ینامز رادقم نیا و
3
رادومن .میشاب هتشاد رتم یتناس 3/5 علض هب عبرم کی ینعی ؛دنشاب رتم یتناس 3/5
2
.دینک هجوت نآ رادومن رد S ممیزکام هطقن هب .تسا هدش مسر زین S عبات
1 ٔ
0
1 2 3 3/5 4 5 6 7 8
)رتم یتناس( لیطتسم علض کی :x

هطقن هک میتسناد یم مه لبق یاه هیاپ زا .دوب ٢ هجرد عبات کی ،میدوب نآ قلطم ممرتسکا رادقم لابند هب هک یعبات ،لبق لاثم رد :رکذت
ٔ
b − −∆
اب .دنتسین ٢ هجرد ،رظندروم یاه عبات هشیمه اما .دهد یم تسد هب ار f )x( = ax + bx + c مود هجرد عبات ممرتسکا هطقن ، ) a 2 , a 4 (
2
ٔ
ّ
.دیهد رارق هجوت دروم ار دعب یاه لاثم .دوب دهاوخ لبق لاثم هباشم راک لحارم ،لاح نیا

114