Page 20 - C112211

عبات ١ لصف

y
4
تیلاعف
3
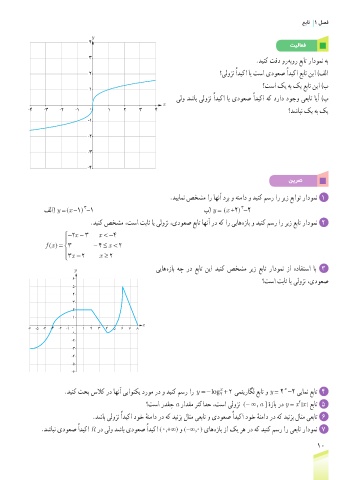
.دینک تقد ور هبور عبات رادومن هب
2 ؟یلوزن ًادیکا ای تسا یدوعص ًادیکا عبات نیا )فلا
؟تسا کی هب کی عبات نیا )ب
1
یلو دشاب یلوزن ًادیکا ای یدوعص ًادیکا هک دراد دوجو یعبات ایآ )پ
x
-4 -3 -2 -1 0 1 2 3 4 4 ؟دشابن کی هب کی
-1

-2

-3

-4
نیرتم

.دییامن صخشم ار اهنآ درب و هنماد و دینک مسر ار ریز عباوت رادومن 1
3
3

فلا( y = )x -1( -1 ب( y = )x +2( -2
.دینک صخشم ،تسا تباث ای یلوزن ،یدوعص عبات اهنآ رد هک ار ییاه هزاب و دینک مسر ار ریز عبات رادومن 2
 − x 2 − 3 x <−4
f x  −≤ < 2
)( =  3
x
4

 x 3 −2 x ≥ 2
y ییاه هزاب هچ رد عبات نیا دینک صخشم ریز عبات رادومن زا هدافتسا اب 3
6
؟تسا تباث ای یلوزن ،یدوعص
5
4
3
2
1
x
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
-1
-2
-3
-4
-5
-6

x
x
.دینک ثحب سلاک رد اهنآ ییاونکی دروم رد و دینک مسر ار =−y log +2 یمتیراگل عبات و y = 2 -2 ییامن عبات 4

2
2
؟تسا ردقچ a رادقم رثکادح ،تسا یلوزن ) - ∞ , a ] هزاب رد y = x |x | عبات 5
ٔ
.دشاب یلوزن ًادیکا دوخ هنماد رد هک دینزب لاثم یعبات و یدوعص ًادیکا دوخ هنماد رد هک دینزب لاثم یعبات 6
ٔ
ٔ
.دشابن یدوعص ًادیکا R رد یلو دشاب یدوعص ًادیکا )0,+∞( و )-∞,0( یاه هزاب زا کی ره رد هک دینک مسر ار یعبات رادومن 7
10