Page 22 - C112211

عبات ١ لصف

(
t d t) = 4t +2 n d t)) = n 4t +2) رادومن نآ کمک هب و دینک لماک ار ور هبور لودج )پ
(
(
(
.دییامن لیمکت ار
0 d 0) = 2 n (d (0)) = n (2) = 420
(
(
(
0/5 d 0/5) = … n (d 0/5)) = n ( … ) = 500
(
(
(
1 d 1) = 6 n (d 1)) = n 6) = …
2 d 2) = … n (d 2)) = n ( … …
(
(
) =
3 d 3) = 14 n (d 3)) = n 14) = 3300
(
(
(
t
t d ( ) n (d(t)) یامد ،نامز نتشاد اب ناوت یم ،میدید هک روط نامه
اه یرتکاب دادعت ،امد نتشاد اب و دروآ تسد هب ار اذغ
0 2 420
0/5 500 .تسا هبساحم لباق
1 6 نتشاد نودب و نامز نتشاد اب ناوت یم امش رظن هب ایآ
2 ؟دروآ تسد هب ار اه یرتکاب دادعت ،امد
3 14 3300
بسحرب ار n هک تخاس یعبات ناوت یم ایآ رگید نایب هب
t
t
t 4 +2 n( 4 +2)
؟دنک صخشم t
:مینک یم لمع ریز تروص هب یعبات نینچ ندروآ تسد هب یارب
2
2
n (d (t )) = n(4t + 2) = 20(4t + 2) - 80(4t + 2) + 500 =………………..………… = 320t +420 0≤ t ≤3
.تسا هدنام نوریب لاچخی زا تعاس t نازیم هب هک دهد یم ناشن ار یلاچخی یاذغ رد دوجوم یاه یرتکاب دادعت n (d (t))

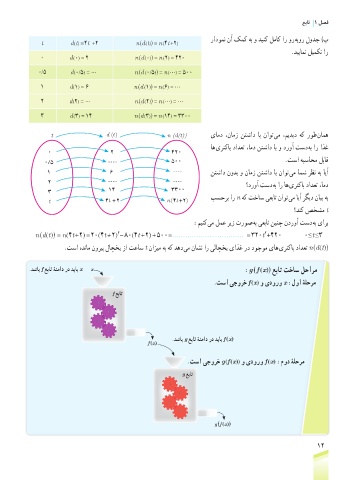
.دشاب f عبات ۀنماد رد دیاب x x :g ( f (x)) عبات تخاس لحارم

.تسا یجورخ f (x) و یدورو x :لوا ۀلحرم
f عبات

.دشاب g عبات ۀنماد رد دیاب f (x)
f (x)

.تسا یجورخ g (f (x)) و یدورو f (x) :مود ۀلحرم

g عبات

g (f (x))

12