Page 23 - C112211

عباوت بیکرت مود سرد

میهد یم شیامن (gof )(x) دامن اب ار g (f (x)) عبات ،دنشاب هتشاد یهتان کارتشا g عبات هنماد و f عبات درب هک یروط هب دنشاب عبات ود g و f رگا
ٔ
(gof ) (x) = g (f (x)) :رگید ترابع هب ،میمان یم بکرم عبات ار gof عبات و

:بکرم عبات ۀنماد

:دننک قدص ریز طرش ود رد نامز مه هک تسا ییاه x هعومجم gof بکرم عبات هنماد
ٔ
.دشاب هتشاد رارق f هنماد رد x ــ1
ٔ
.دشاب هتشاد رارق g هنماد رد f (x) ــ2
ٔ
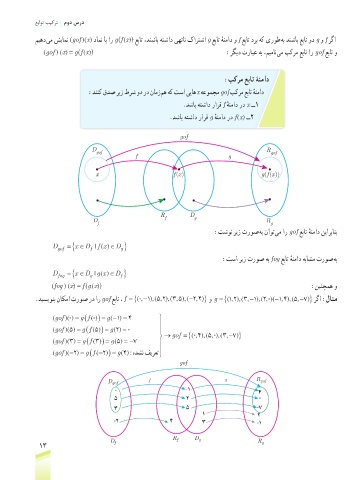
gof

D R
gof gof
f g

x fx() gf x))
(
(

R D
D f g R
f g
:تشون ریز تروص هب ناوت یم ار gof عبات هنماد نیاربانب
ٔ
= { ∈ D x | ()∈D f x D }
gof f g
:تسا ریز تروص هب fog عبات هنماد هباشم تروص هب
ٔ
= { ∈ D x | ()∈D gx D }
fog g f
(fog ) (x) = f (g (x)) :نینچمه و
.دیسیونب ناکما تروص رد ار gof عبات ، f = {( ,− 0 ),( , ),( , ),( 24 } ) و = g {( , ),( ,−12 3 ),( , )( , ),( ,−14 5 } ) 7 رگا :لاثم
,
5
2
3
5
−1
20
−1
)
)() = g f 0
(gof 0 ( () = g ( ) = 4 
−1

( ) =0
)() = g
(gof 5 ( () =f 5 ) g 2  → = gof 04 5 } )
)
( ) = −7
)() = g f 3
(gof 3 ( () = g 5  {( , ),( , ),( ,− 0 3 7

( ):
(gof )(−2 ) = g f ) ) = g 4 هدشن فیرعت 
( (−2

gof
D gof f g R gof
0 -1 4
5 2 0
3 5 -7
1 2
-2 4 3 -1
R D
D f f g R g
13