Page 28 - C112211

عبات ١ لصف

(
(
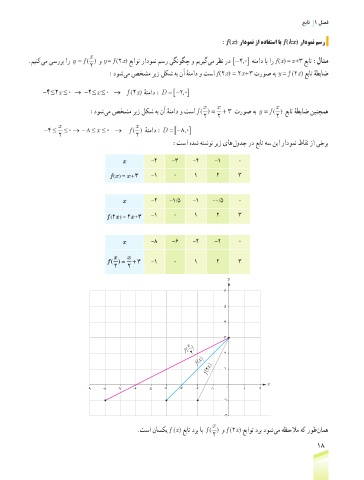
:f x) رادومن زا هدافتسا اب f kx) رادومن مسر
x
y
] ,0
.مینک یم یسررب ار = f () و y = f (2x) عباوت رادومن مسر یگنوگچ و میریگ یم رظن رد [−4 هنماد اب ار f (x) = x +3 عبات :لاثم
2
:دوش یم صخشم ریز لکش هب نآ هنماد و تسا f (2x) = 2x + 3 تروص هب y = f (2x) عبات هطباض
ٔ
ٔ
-4 ≤ 2x ≤ 0 → -2 ≤ x ≤ 0 → f (2x) هنماد :D = [−20 ] ,
ٔ
x x x
:دوش یم صخشم ریز لکش هب نآ هنماد و تسا () = 2 + 3 تروص هب y = f () عبات هطباض نینچمه
f
ٔ
ٔ
2
2
x x
− ≤ ≤ →− ≤ x ≤0 → ()f هنماد :D = [−80 ] ,
4
0
8
ٔ
2 2
:تسا هدش هتشون ریز یاه لودج رد عبات هس نیا رادومن طاقن زا یخرب
x -4 -3 -2 -1 0
(
f x ) = x + 3 -1 0 1 2 3
x -2 -1/5 -1 -0/5 0

(
f 2x ) = 2x +3 -1 0 1 2 3

x -8 -6 -4 -2 0
x x
f () = + 3 -1 0 1 2 3
2 2

y

6

5

4

3
x )
f ( 2 2

f (x ) )
(2 x 1
f
x
-9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2
-1

-2
x

.تسا ناسکی f (x) عبات درب اب () و f (2x) عباوت درب دوش یم هظحلام هک روط نامه
f
2
18