Page 29 - C112211

عباوت بیکرت مود سرد

1
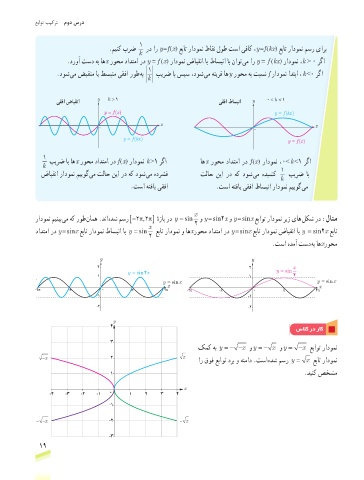
.مینک برض رد ار y =f (x) عبات رادومن طاقن لوط تسا یفاک ،y =f (kx) عبات رادومن مسر یارب
k
.دروآ تسد هب اهx روحم دادتما رد y = f (x) رادومن ضابقنا ای طاسبنا اب ناوت یم ار y = f (kx) رادومن ،k < ٠ رگا
1
.دوش یم ضبقنم ای طسبنم یقفا روط هب بیرض اب سپس ،دوش یم هنیرق اه y روحم هب تبسن f رادومن ادتبا ، k >0 رگا
k

k >1
y
یقفا ضابقنا یقفا طاسبنا y < 0 k < 1
y = fx y = f ()
()
kx
x x
0 0
y = f () y = fx
kx
()
1
بیرض اب اه x روحم دادتما رد f (x) رادومن k <1 رگا اه x روحم دادتما رد f (x) رادومن ،0> k >1 رگا
k
1
ضابقنا رادومن مییوگ یم تلاح نیا رد هک دوش یم هدرشف تلاح نیا رد هک دوش یم هدیشک بیرض اب
k
.تسا هتفای یقفا .تسا هتفای یقفا طاسبنا رادومن مییوگ یم

y
2
y =
x
2
sin x
]
,
رادومن مینیب یم هک روط نامه .دنا هدش مسر[−π π22 هزاب رد y = sin و y = sin2x و y = sinx عباوت رادومن ریز یاه لکش رد :لاثم
1
ٔ
x 2 y = sinx
x
دادتما رد y = sinx عبات رادومن طاسبنا اب y = sin عبات رادومن و اهxروحم دادتما رد y = sinx عبات رادومن ضابقنا اب y = sin2x عبات
2π
-π
0
π
-2π
2 -1
.تسا هدمآ تسد هب اهxروحم
-2
y y
2 2 x
y = sin x y = sin
2
1 1 2
y = sinx y = sinx
-2π -π 0 π 2π x -2π -π 0 π 2π x
-1 -1
-2 -2
y y
2 4 x
y = sin سلاک رد راک
1 2
3 y = sinx
x
y
y
-2π -π 0 π 2π کمک هب = − −y x و = − x و = −x عباوت رادومن
x − -1 2 x ار قوف عباوت درب و هنماد .تسا هدش مسر y = x عبات رادومن
-2
1 .دینک صخشم
x
-4 -3 -2 -1 0 1 2 3 4 4
-1
−− x -2 − x
-3
19