Page 34 - C112211

عبات ١ لصف

موس سرد

نوراو عبات

یروآدای

هک دیآ یم تسد هب دیدج یعبات ،f کی هب کی عبات بترم یاه جوز یاه هفلؤم ندرک اج هباج اب میدید 2 یضایر باتک عبات لصف رد هک روط نامه
-1
رادومن یور (b , a) هطقن هاگ نآ دشاب هتشاد رارق f عبات رادومن یور (a , b) هطقن رگا ینعی .میهد یم ناشن f اب ار نآ و تسا f عبات نوراو
ٔ
ٔ
-1
:سکع هب و دراد رارق f عبات
(a , b) ∈ f ⇔ (b , a) ∈ f -1
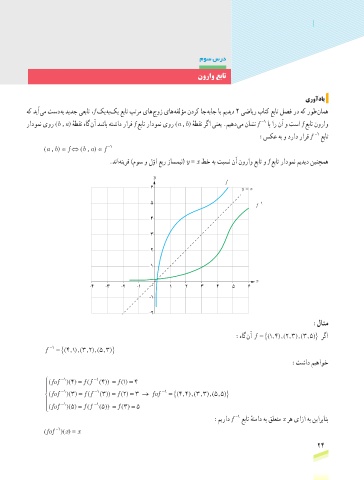
.دنا هنیرق )موس و لوا عبر زاسمین( y = x طخ هب تبسن نآ نوراو عبات و f عبات رادومن میدید نینچمه
ّ
y
f
6 y = x

5 f −1

4

3

2

1

x
-4 -3 -2 -1 0 1 2 3 4 4 5 6

-1

-2
:لاثم
:هاگ نآ f = {( , ),( , ),( , )14 2 3 3 5 } رگا

f −1 = {( , ),( , ),( , )41 3 2 5 3 }

:تشاد میهاوخ

 (fof − )( ) = ( f f −1 1 ( )) = 1
4
( ) = 4
f
4
 − −

 (fof )() = 3 ( f f −1 1 ()) = 3 f ( ) = 3 →2 fof 1 = {(, ),( , ),( , )44 3 3 5 5 }
 − −1 1
5
5
( ) = 5
  (fof )( ) = ( f f ( )) = f 3
-1
:میراد f عبات هنماد هب قلعتم x ره یازا هب نیاربانب
ٔ
-1
(fof )(x) = x
24