Page 35 - C112211

نوراو عبات موس سرد

:نینچمه
−
 (f of 1 f −1 ( ( )) = f − 1 1 ( ) =1
)( ) =
4
f 1


−
)( ) =
 (f of 2 f −1 ( ( )) = f 2 f − 1 1 ( ) = 2 →3 f of = − 1 {( , ),( , ),( , )11 2 2 3 3 }
 − −1 −1 1
)( ) =
5
f 3
  (f of 3 f ( ( )) = f ( ) = 3
-1
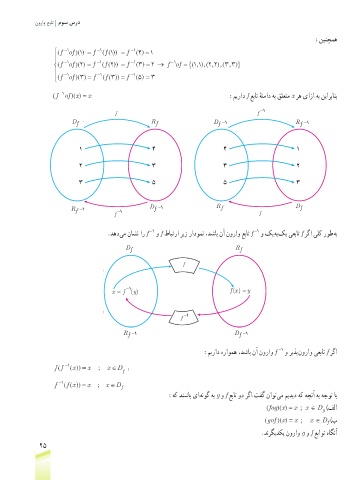
( f of )(x) = x :میراد f عبات هنماد هب قلعتم x ره یازا هب نیاربانب
ٔ
−1
f f
D f R f D f −1 R f −1
1 4 4 1
2 3 3 2

3 5 5 3

R f −1 −1 D f −1 R f D f
f f

-1
-1
.دهد یم ناشن ار f و f طابترا ریز رادومن ،دشاب نآ نوراو عبات f و کی هب کی یعبات f رگا یلک روط هب
D f R f

f

() =
x = f −1 () fx y
y

−1
f

R f −1 D f −1

-1
:میراد هراومه ،دشاب نآ نوراو f و ریذپ نوراو یعبات f رگا
=
( ff −1 ( )) x ; x ∈ D −1
x
f
=
f −1 ( ( )) x ; x ∈ D f
f
x
:هک دنشاب یا هنوگ هب g و f عبات ود رگا تفگ ناوت یم میدید هک هچنآ هب هجوت اب
(fog)(x) = x ; x ∈ D )فلا
g
(gof )(x) = x ; x ∈ D )ب
f
.دنرگیدکی نوراو g و f عباوت هاگنآ
25