Page 37 - C112211

نوراو عبات موس سرد

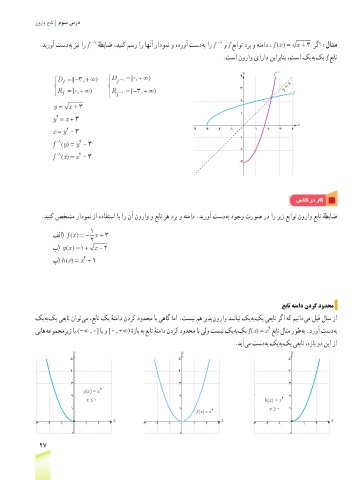
.دیروآ تسد هب زین ار f هطباض ،دینک مسر ار اهنآ رادومن و هدروآ تسد هب ار f و f عباوت درب و هنماد ، () = x + 3 رگا :لاثم
-1
-1
x
f
ٔ
.تسا نوراو یاراد نیاربانب ،تسا کی هب کی f عبات
y f −1
0
,
D f = [− +∞ ) D f − = [ ,+∞ ) 4
3


1
  3 y = x
[ ,+∞
R
, 3
  f = 0 )  R − = [− +∞ ) f
1
 f
2
y = x + 3
1
2
y = x + 3
x
2
x = y - 3 -4 -3 -2 -1 0 1 2 3 4 4
-1
2
-1
f (y) = y - 3
-2
-1
2
f (x) = x - 3
-3
سلاک رد راک
.دینک صخشم رادومن زا هدافتسا اب ار نآ نوراو و عبات ره درب و هنماد .دیروآ تسد هب دوجو تروص رد ار ریز عباوت نوراو عبات هطباض
ٔ
1
فلا( ()f x = − x + 3
2
ب( ()gx = 1 + x − 2
2
پ( h (x) = x + 1

عبات هنماد ندرک دودحم

کی هب کی یعبات ناوت یم ،عبات کی هنماد ندرک دودحم اب یهاگ اما .تسین مه ریذپ نوراو دشابن کی هب کی یعبات رگا هک میناد یم لبق لاس زا
ٔ
2
ییاه هعومجمریز ای (- ∞ , 0] ای و [0 , + ∞) هزاب هب عبات هنماد ندرک دودحم اب یلو تسین کی هب کی f (x) = x عبات لاثم روط هب .دروآ تسد هب
ٔ ٔ
.دیآ یم تسد هب کی هب کی یعبات ،هزاب ود نیا زا
y y y
5 5 5

4 4 4
3 3 3
() =
gx x 2
2 2 2 2
() =
x ≤0 hx x
1 1 2 x ≥0 1
=
f(x) x
x x x
-3 -2 -1 0 1 2 3 -3 -2 -1 0 1 2 3 -3 -2 -1 0 1 2 3
-1 -1 -1
27