Page 46 - C112211

تاثلثم 2 لصف

y
2

1
1
2
x )ب
−π −π −π −π 0 π 2 π π 4 π 5 π 2 π
4
5
2
-2 π 3 3 - π 3 3 − 1 3 3 3 3
2
-1
-2
y
5
4
3
2 )پ
1
x
-2π -π 0 π 2π 3π 4π 5π 6π
-1
-2
-3
y
4
3

2
1 )ت
x
-2π 3 π -π π 0 π π 3 π 2π 5 π 3π 7 π 4π 9 π 5π 11 π 6π
- -
2 2 -1 2 2 2 2 2 2
-2
-3

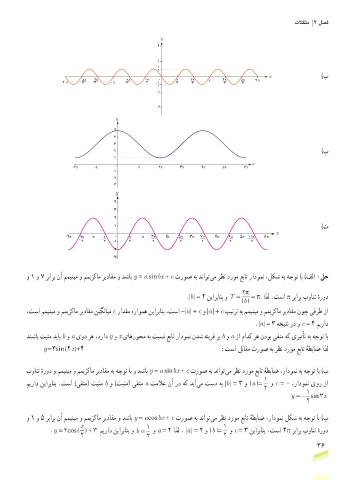
و 1 و 7 ربارب نآ ممینیم و ممیزکام ریداقم و دشاب y = a sin bx + c تروص هب دناوت یم رظن دروم عبات رادومن ،لکش هب هجوت اب )فلا :لح

2 π
.|b = 2 نیاربانب و T = =π اذل .تسا π ربارب بوانت هرود
|
|| ٔ
b
،تسا ممینیم و ممیزکام ریداقم نیگنایم c رادقم هراومه نیاربانب ،تسا -|a | + c و |a | + c بیترت هب ممینیم و ممیزکام ریداقم نوچ یفرط زا
.|a | = 3 هجیتن رد و c = 4 میراد
دنشاب تبثم دیاب b و a یود ره ،دراد y و x یاهروحم هب تبسن عبات رادومن ندش هنیرق رب b و a زا مادک ره ندوب یفنم هک یریثأت هب هجوت اب

y = 3sin (2 x) +٤ :تسا لباقم تروص هب رظن دروم عبات هطباض اذل
ٔ

بوانت هرود و ممینیم و ممیزکام ریداقم هب هجوت اب و دشاب y = a sin bx + c تروص هب دناوت یم رظن دروم عبات هطباض ،رادومن هب هجوت اب )ب
ٔ ٔ
1
میراد نیاربانب .تسا )یفنم( تبثم b و )تبثم( یفنم a تملاع نآ رد هک دیآ یم تسد هب |b | = 3 و ||a = و c = 0 ،رادومن یور زا
2 1
y =− sin x
3
2
و 1 و 5 ربارب نآ ممینیم و ممیزکام ریداقم و دشاب y = a cos bx + c تروص هب دناوت یم رظن دروم عبات هطباض ،رادومن لکش هب هجوت اب )پ
ٔ
x 1 1
.y = 2 cos( ) + 3 میراد نیاربانب و b = و a = 2 اذل . |a | = 2 و ||b = و c = 3 نیاربانب .تسا 4π ربارب بوانت هرود
2 2 2 ٔ
36