Page 49 - C112211

تناژنات و بوانت لوا سرد

تناژنات عبات
π
و میراد tanx ناونع هب یقیقح یددع ،)x = kπ+ , ∈ زج هب( یتاثلثم هریاد رد هاوخلد هیواز ره یازا هب مینیب یم هک روط نامه
k
ٔ
2 ٔ
 π 

دادعا هعومجم نآ درب و تسا D =  x ∈ x ≠ kπ+ , k ∈  هعومجم عبات نیا هنماد .دنک یم صخشم y = tan x هطباض اب یعبات
ٔ
ٔ
ٔ
 2 
1
:اریز ،تسا π نآ بوانت هرود و تسا بوانتم یعبات ،y = tan x عبات دید ناوت یم یگداس هب .تسا یقیقح
tan (π + x) = tan x
سلاک رد راک

 π 3 π
.دینک یسررب [0 , 2π] −  ,  ٔ هعومجم رد ار y = tanx عبات ندوب یلوزن ای یدوعص
 22 

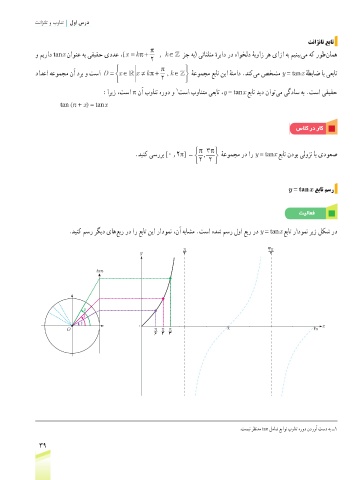
y = tan x عبات مسر

تیلاعف

.دینک مسر رگید یاه عبر رد ار عبات نیا رادومن ،نآ هباشم .تسا هدش مسر لوا عبر رد y = tan x عبات رادومن ریز لکش رد

π 3 π
y 2 2

tan

π
3
π
4
π
6 0 x
O π π π π 2π
6 4 3

.تسین رظندم tan لماش عباوت بوانت هرود ندروآ تسد هب ــ1

39