Page 64 - C112211

تیاهن یب رد دح و تیاهن یب دح 3 لصف

یگیاسمه کی (x , x + r) هاگنآ دشاب تبثم یددع r رگا :تسار و پچ یگیاسمه
0
0
.میمان یم x پچ یگیاسمه کی ار (x - r , x ) ،نینچمه .دوش یم هدیمان x تسار
0
0
0
0
3
کی و 3 یارب رگید تسار یگیاسمه کی امش .تسا 3 پچ یگیاسمه کی ( ,) 3 هزاب و 3 تسار یگیاسمه کی (3 , 4) هزاب :لاثم
2 ٔ ٔ
.دیسیونب نآ یارب پچ یگیاسمه

x
0 1 3 2 3 4 5 6
2

تیلاعف

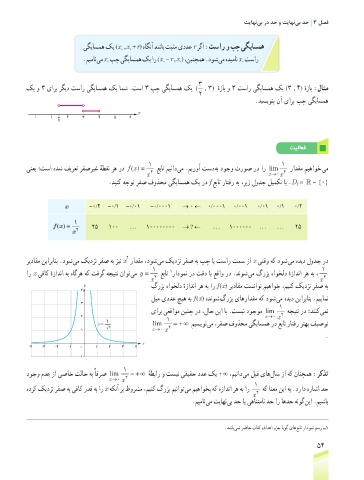
1 1
ینعی ؛تسا هدش فیرعت رفصریغ هطقن ره رد () = عبات میناد یم .میروآ تسد هب دوجو تروص رد ار lim رادقم میهاوخ یم
x
f
ٔ
x 2 x→0 x 2
.دینک هجوت رفص فوذحم یگیاسمه کی رد f عبات راتفر هب ،ریز لودج لیمکت اب .D f =  - {0}
x -0/2 -0/1 -0/01 -0/0001 → 0 ← 0/0001 0/001 0/01 0/1 0/2

1
() =
fx 25 100 ... 100000000 → ? ← ... 1000000 ... ... 25
x 2

2
ریداقم نیاربانب .دوش یم کیدزن رفص هب زین x رادقم ،دوش یم کیدزن رفص هب پچ ای تسار تمس زا x یتقو هک دوش یم هدید لودج رد
1 1
ار x یفاک هزادنا هب هاگره هک تفرگ هجیتن ناوت یم y = عبات رادومن رد تقد اب عقاو رد .دنوش یم گرزب هاوخلد هزادنا ره هب ،
١
ٔ x 2 ٔ x 2
گرزب هاوخلد هزادنا ره هب ار f (x) ریداقم تسناوت میهاوخ ،مینک کیدزن رفص هب
4 ٔ
لیم یددع چیه هب f (x) هدنوش گرزب یاهرادقم هک دوش یم هدید نیاربانب .مییامن
3 1
یارب یعقاوم نینچ رد ،لاح نیا اب .تسین دوجوم lim هجیتن رد ؛دننک یمن
2 1 x→0 x 2
= lim = +∞ میسیون یم ،رفص فوذحم یگیاسمه رد عبات راتفر رتهب فیصوت
1 x→0 x 2
.

-4 -3 -2 -1 0 1 2 3 4
-1
1
دوجو مدع زا یصاخ تلاح هب ًافرص lim = +∞ هطبار و تسین یقیقح ددع کی + ∞ ،میناد یم لبق یاه لاس زا هک نانچمه :رکذت
ٔ
x→0 x 2
هدرک کیدزن رفص هب یفاک ردق هب ار x هکنآ رب طورشم ،مینک گرزب میناوت یم میهاوخب هک هزادنا ره هب ار 1 هک انعم نیا هب .دراد هراشا دح
x 2
.میمان یم تیاهن یب دح ای یهانتمان دح ار اهدح هنوگ نیا .میشاب

.دشاب یمن رضاح باتک فادها وزج ایوگ یاه عبات رادومن مسر ــ١

54