Page 68 - C112211

تیاهن یب رد دح و تیاهن یب دح 3 لصف

مود سرد

تیاهن یب رد دح

تیاهن یب رد دح

لیم - ∞ ای + ∞ هب y ریداقم ،دش یم کیدزن a لثم یددع تمس هب x یتقو هک میدید ،میدرک یسررب ار یهانتمان یاهدح هک لبق سرد رد
.میروآ یم تسد هب دوجو تروص رد ار عبات دح و میهد یم لیم - ∞ ای + ∞ هب ار x اجنیا رد .درک یم

تیلاعف

گنر ار عبرم حطس فصن ،لوا هلحرم رد .مینک گنر ریز یاه لکش قباطم یدنیارف یط ار رتم 1 علض هب یعبرم حطس میهاوخب دینک ضرف
ّ ٔ
.میهد یم همادا بیترت نیمه هب و مینز یم گنر ار هدشن گنر یاه تمسق فصن مود هلحرم رد .مینک یم
ٔ

هلحرم 1 2 3 4 ...

لکش ...

1 1 3 1 7 1
1
1
1
)عبرم رتم( هدش گنر حطس = − = − = − ... ...
2 2 4 2 2 8 2 3
؟تسا هدش گنر عبرم زا یحطس هچ ،مهد هلحرم رد )فلا
ٔ
؟تسا هدش گنر عبرم زا یحطس هچ ،ما n هلحرم رد )ب
ٔ
؟تفگ ناوت یم هچ ما n هلحرم رد هدش گنر حطس تحاسم دروم رد ،دوش رایتخا گرزب یفاک ردق هب n رگا )پ
ٔ
y
4
1
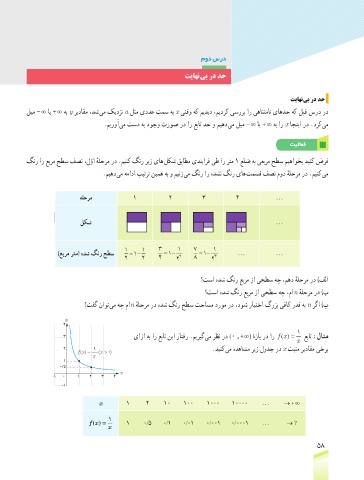
3 یازا هب ار عبات نیا راتفر .میریگ یم رظن رد (0 , + ∞) هزاب رد ار ()f x = عبات :لاثم
ٔ x
2 1 .دینک یم هدهاشم ریز لودج رد x تبثم ریداقم یخرب
() =
fx (x >0 )
x
1
0/5
x
-1 0 1 2 3 4
-1

x 1 2 10 100 1000 10000 ... → + ∞

1
() =
fx 1 0/5 0/1 0/01 0/001 0/0001 ... → ?
x
58