Page 72 - C112211

تیاهن یب رد دح و تیاهن یب دح 3 لصف

سلاک رد راک

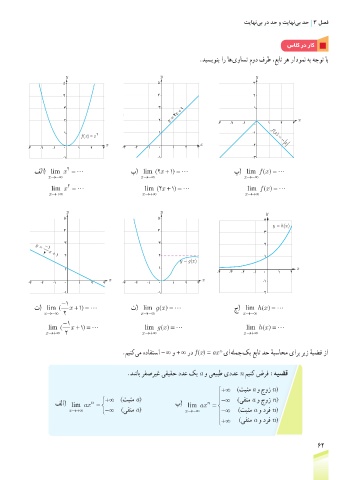
.دیسیونب ار اه یواست مود فرط ،عبات ره رادومن هب هجوت اب

y y y
5 5 3

4 4 2
3 3 x +1 1
y = 2
2 2 -3 -2 -1 0 1 2 3 x
f
1 2 1 -1 (x
=
f(x) x ) = −
x x -2 x
-3 -2 -1 0 1 2 3 -3 -2 -1 0 1 2 3
-1 -1 -3
2
فلا( lim x =  ب( lim ( x +2 ) =1  پ( lim f ( ) = 
x
x→−∞ x→−∞ x→−∞
2
lim x =  lim ( x +2 ) =1  lim f ( ) = 
x
x→+∞ x→+∞ x→+∞
y y y
5 5 4
y = hx
()
4 4 3
3 3 2
y =
−1
2 x +1
2 2 1
y = gx
()
1 1 x
-4 -3 -2 -1 0 1 2
x x -1
-3 -2 -1 0 1 2 3 -3 -2 -1 0 1 2 3
-1 -1 -2
−1
ت( lim ( x + ) =1  ث( lim gx =  ج( lim hx = 
( )
( )
x→−∞ 2 x→−∞ x→−∞
−1
lim ( x + ) =1  lim gx =  lim hx = 
( )
( )
x→+∞ 2 x→+∞ x→+∞
n
.مینک یم هدافتسا - ∞ و + ∞ رد f (x) = ax یا هلمج کی عبات دح هبساحم یارب ریز هیضق زا
ٔ
ٔ
.دشاب رفصریغ یقیقح ددع کی a و یعیبط یددع n مینک ضرف :هیضق

 +∞ (تبثم a و جوز n)
 +∞ (تبثم a)  −∞ (یفنم a و جوز n)

n
n

فلا( lim ax =  ب( lim ax = 
x→+∞  −∞ (یفنم a) x→−∞  −∞ (تبثم a و درف n)
 +∞ (یفنم a و درف n)

6٢