Page 74 - C112211

تیاهن یب رد دح و تیاهن یب دح 3 لصف

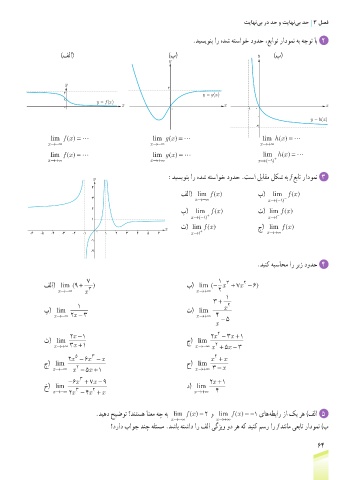
.دیسیونب ار هدش هتساوخ دودح ،عباوت رادومن هب هجوت اب 2

)فلا( )ب( )پ(
y
y

y
2
2 y = gx
()
1 y = fx
()
0 x 0 x -1 0 x
()
y = hx
-2
( )
( ) 
lim f ( ) =  lim gx =  lim hx =
x
x→−∞ x→−∞ x→+∞
( )
( )
lim f ( ) =  lim gx =  lim hx = 
x
x→+∞ x→+∞ x→−1 ) +
(
y :دیسیونب ار هدش هتساوخ دودح .تسا لباقم لکش هب f عبات رادومن 3
4
x
فلا( lim f ( ) ب( lim f ( )
x
3 x→−∞ x→−1 ) −
(
2 پ( lim f ( ) ت( lim ( )
x
x
f
(
x→−1 ) + x→1 −
1
ث( lim ( ) ج( lim f ( )
x
x
f
x
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 x→1 + x→+∞
-1
-2
.دینک هبساحم ار ریز دودح 4
7 1 3 2
فلا( lim ( + ) ب( lim (− x + 7 x − ) 6
9
x→−∞ x 3 x→+∞ 2
3 + 1
1 x 2
پ( lim ت( lim
x→−∞ 2 x − 3 x→+∞ 4 −5
x
2
2 x −1 2 x − 3 x +1
ث( lim ج( lim
x→+∞ 3 x +1 x→−∞ x + 5 x − 3
2
5
3
2
2 x −6 x − x x + x
چ( lim ح( lim
2
x→−∞ x −5 x +1 x→+∞ 3 − x
3
−6 x + 7 x −9 2 x +1
خ( lim د( lim
2
3
x→−∞ 2 x −4 x + x x→+∞ 4
x
x
.دیهد حیضوت ؟دنتسه انعم هچ هب lim f ( ) = 2 و lim f ( ) =−1 یاه هطبار زا کی ره )فلا 5
x→−∞ x→+∞
؟دراد باوج دنچ هلئسم .دشاب هتشاد ار فلا یگژیو ود ره هک دینک مسر ار f دننام یعبات رادومن )ب
6٤