Page 88 - C112211

قتشم 4 لصف

سلاک رد راک

y
4 x 2 x ≤1
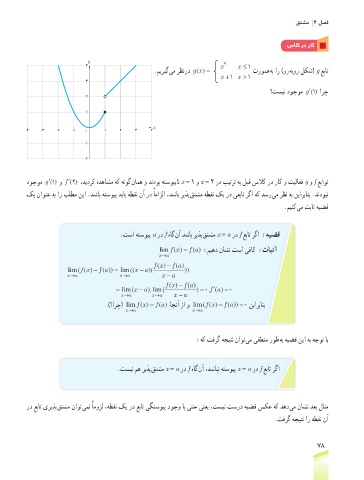
.میریگ یم رظنرد ()gx = تروص هب ار )ور هبور لکش( g عبات
x + x >1 1
3
؟تسین دوجوم ()1g ′ ارچ
2

1

x
-4 -3 -2 -1 0 1 2 3 4
-1

-2

دوجوم ()1g ′ و ()2f ′ ،دیدرک هدهاشم هک هنوگ نامه و دندوب هتسویپان x = 1 و x = 2 رد بیترت هب لبق سلاک رد راک و تیلاعف g و f عباوت

کی ناونع هب ار بلطم نیا .دشاب هتسویپ دیاب هطقن نآ رد ًامازلا ،دشاب ریذپ قتشم هطقن کی رد یعبات رگا هک دسر یم رظن هب نیاربانب .دندوبن
.مینک یم تباث هیضق

.تسا هتسویپ a رد f هاگ نآ دشاب ریذپ قتشم x = a رد f عبات رگا :هیضق

( )
f
x
lim ( ) = fa :میهد ناشن تسا یفاک :تابثا
x →a
−
()
x
f ( ) fa
lim( ( ) x − f fa lim((x a )( ))
( )) =
−
−
x→ a x→ a xa
()
−
f ( ) fa
x
′
= lim(x a ).lim( ) = 0 . ( ) = fa 0
−
−
x→ a x→ a xa
)؟ارچ( lim ( ) =f x fa ( )) = fa 0 نیاربانب
( ) اجنآ زا و lim( ( ) − f x
x →a x →a
:هک تفرگ هجیتن ناوت یم یقطنم روط هب هیضق نیا هب هجوت اب
.تسین مه ریذپ قتشم x = a رد f هاگ نآ ،دشابن هتسویپ x = a رد f عبات رگا

رد عبات یریذپ قتشم ناوت یمن ًاموزل ،هطقن کی رد عبات یگتسویپ دوجو اب یتح ینعی ،تسین تسرد هیضق سکع هک دهد یم ناشن دعب لاثم

.تفرگ هجیتن ار هطقن نآ

78